業務分析・データ利活用(全119問中43問目)

No.43解説へ
ある工場では表に示す3製品を製造している。実現可能な最大利益は何円か。ここで,各製品の月間需要量には上限があり,また,組立て工程に使える工場の時間は月間200時間までで、複数種類の製品を同時に並行して組み立てることはできないものとする。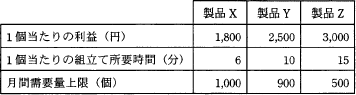

出典:平成26年春期 問71
- 2,625,000
- 3,000,000
- 3,150,000
- 3,300,000
正解 エ問題へ
広告
解説
この問題のように最適な製品ミックスが問われた場合、まず先に行うことは作業時間当たりの利益が最も高い製品を明らかにすることです。
[製品X] 1,800÷ 6=300
[製品Y] 2,500÷10=250
[製品Z] 3,000÷15=200
作業時間当たりの利益が最も多いのは、製品Xであることがわかりました。これにより製品Xを優先させて製造することが、最大利益を上げるために必要な条件であることになります。
製造に使える時間は最大で200時間なので、まず製品Xを需要MAXの1,000個製造します。
200-(6×1,000÷60)=100
まだ製造時間が100時間あるので、続いて利益率が高い製品Yを製造します。製品Yに100時間の製造時間を割り当てると、
(10×n)/60=100
10n=6,000
n=600
の計算から、600個の製品Yが製造可能であることがわかります。
最後に、製品X1,000個と、製品Y600個製造した時の予想利益を計算すると、
(1,800×1,000)+(2,500×600)=3,300,000
となるので、実現可能な予想利益は 3,300,000円となります。
[製品X] 1,800÷ 6=300
[製品Y] 2,500÷10=250
[製品Z] 3,000÷15=200
作業時間当たりの利益が最も多いのは、製品Xであることがわかりました。これにより製品Xを優先させて製造することが、最大利益を上げるために必要な条件であることになります。
製造に使える時間は最大で200時間なので、まず製品Xを需要MAXの1,000個製造します。
200-(6×1,000÷60)=100
まだ製造時間が100時間あるので、続いて利益率が高い製品Yを製造します。製品Yに100時間の製造時間を割り当てると、
(10×n)/60=100
10n=6,000
n=600
の計算から、600個の製品Yが製造可能であることがわかります。
最後に、製品X1,000個と、製品Y600個製造した時の予想利益を計算すると、
(1,800×1,000)+(2,500×600)=3,300,000
となるので、実現可能な予想利益は 3,300,000円となります。
広告