令和元年秋期試験午後問題 問2

問2 ソフトウェア
スレッドを使用した並列実行に関する次の記述を読んで,設問1~3に答えよ。
プログラム中の並列実行が可能な部分を取り出し,その部分を分割して複数のスレッドで並列に実行する方法(以下,スレッド並列法という)がある。マルチプロセッサシステムでは,スレッド並列法を適用することによって,プログラムの実行時間を短縮できることがある。
プログラムにおいて,スレッド並列法を適用しないで実行したときの実行時間を,スレッド並列法を適用したときの実行時間で割った値を,プログラム実行時間の高速化率という。
プログラムをスレッド並列法を適用しないで実行したときの,プログラム全体の実行時間に対する,並列実行可能な部分の実行時間の割合を r(0≦r≦1) とする。スレッドの個数を n(n≧1) にして,プログラムにスレッド並列法を適用すると,マルチプロセッサシステムでは,プログラム実行時間の高速化率 E は,次の式で求められる。ここで,各スレッドはそれぞれ異なるプロセッサに割り当てられるものとし,プログラムの実行に使用する全てのプロセッサの性能は同じとする。
E=1(1-r)+rn
この式は,並列実行可能な部分のプログラム実行時間がスレッド並列法の適用によって 1n になり,その他の部分のプログラム実行時間は変化しないときの高速化率を計算するものである。
プログラム中に並列実行が可能な部分をもつプログラムAに対してスレッドの個数を2にしてスレッド並列法を適用すると,高速化率は 32 になった。この場合,rはaである。
rが 34 であるプログラムBの場合,スレッドの個数を増やしても,高速化率の上限はbである。
プログラム中の並列実行が可能な部分を取り出し,その部分を分割して複数のスレッドで並列に実行する方法(以下,スレッド並列法という)がある。マルチプロセッサシステムでは,スレッド並列法を適用することによって,プログラムの実行時間を短縮できることがある。
プログラムにおいて,スレッド並列法を適用しないで実行したときの実行時間を,スレッド並列法を適用したときの実行時間で割った値を,プログラム実行時間の高速化率という。
プログラムをスレッド並列法を適用しないで実行したときの,プログラム全体の実行時間に対する,並列実行可能な部分の実行時間の割合を r(0≦r≦1) とする。スレッドの個数を n(n≧1) にして,プログラムにスレッド並列法を適用すると,マルチプロセッサシステムでは,プログラム実行時間の高速化率 E は,次の式で求められる。ここで,各スレッドはそれぞれ異なるプロセッサに割り当てられるものとし,プログラムの実行に使用する全てのプロセッサの性能は同じとする。
E=1(1-r)+rn
この式は,並列実行可能な部分のプログラム実行時間がスレッド並列法の適用によって 1n になり,その他の部分のプログラム実行時間は変化しないときの高速化率を計算するものである。
プログラム中に並列実行が可能な部分をもつプログラムAに対してスレッドの個数を2にしてスレッド並列法を適用すると,高速化率は 32 になった。この場合,rはaである。
rが 34 であるプログラムBの場合,スレッドの個数を増やしても,高速化率の上限はbである。
広告
設問1
本文中の に入れる正しい答えを,解答群の中から選べ。
a に関する解答群
- 16
- 14
- 13
- 12
- 23
b に関する解答群
- 2
- 3
- 4
- 6
- 8
解答選択欄
- a:
- b:
- a=オ
- b=ウ
解説
〔aについて〕設問で与えられている高速化率を求める式のn(スレッドの個数)に2を、Eに 32 を代入してrを求めます。
32=1(1-r)+r2
32=22(1-r)+r
32=22-2r+r
32=22-r
3(2-r)=4
6-3r=4
-3r=-2
r=23
並列実行可能な部分の割合を表すrは 23 とわかります。
∴a=オ:23
〔bについて〕
高速化率を求める式のrに 34 を代入すると次の式が得られます。ここでは連分数を避けるために 34=0.75 を使って計算しています。
E=1(1-0.75)+0.75n
E=10.25+0.75n
高速化率を大きくするためには分母を小さくする必要がありますが、上記の式を見るとnがどれだけ大きくなっても分母が0.25より小さな値になることはありません。したがって「1÷0.25=4」が、rが 34 の場合における高速化の上限となります。
∴b=ウ:4
広告
設問2
次の記述中の に入れる正しい答えを,解答群の中から選べ。
配列の操作を行う繰返しの処理において,図1,図2のように繰返しの範囲を分割して,スレッド並列法を適用することを考える。
このとき,操作の内容によって,正しい結果が得られる場合と得られない場合があるので,十分に検討することが必要である。
正しい結果が得られる場合の例を,図1に示す。
図1に示すプログラム1は,制御変数 i の取る範囲を分けることによって繰返し範囲を分割した繰返しの処理を,それぞれ異なるスレッドで実行できる。
なお,図1,図2において,実線の四角はプログラム,破線の四角は繰返しの処理,破線の四角から出る二つの矢印は分割を示す。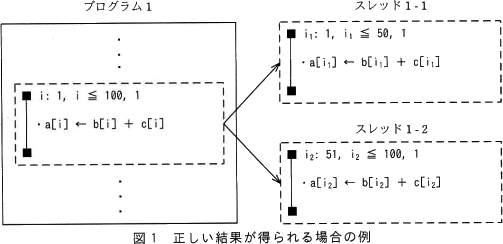 正しい結果が得られない場合の二つの例を,図2に示す。
正しい結果が得られない場合の二つの例を,図2に示す。
プログラム2の繰返しの処理を,スレッド2-1とスレッド2-2の二つに分割すると,cことがあるので,スレッド並列法を適用しない場合の実行結果と等しくなることを保証できない。したがって,プログラム2に対しては,繰返しの範囲の分割によるスレッド並列法を適用できない。
また,プログラム3の繰返しの処理を,スレッド3-1とスレッド3-2の二つに分割すると,dことがあるので,スレッド並列法を適用しない場合の実行結果と等しくなることを保証できない。したがって,プログラム3に対しても,繰返しの範囲の分割によるスレッド並列法を適用できない。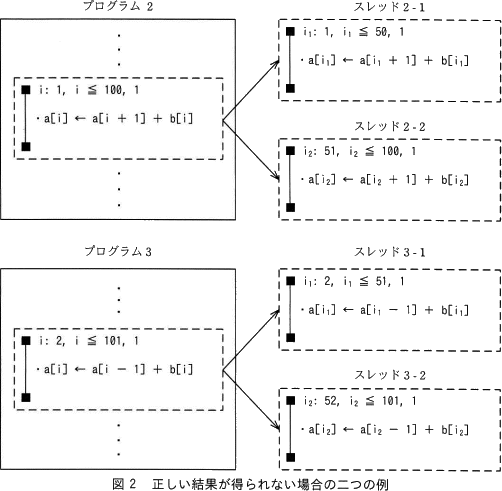
配列の操作を行う繰返しの処理において,図1,図2のように繰返しの範囲を分割して,スレッド並列法を適用することを考える。
このとき,操作の内容によって,正しい結果が得られる場合と得られない場合があるので,十分に検討することが必要である。
正しい結果が得られる場合の例を,図1に示す。
図1に示すプログラム1は,制御変数 i の取る範囲を分けることによって繰返し範囲を分割した繰返しの処理を,それぞれ異なるスレッドで実行できる。
なお,図1,図2において,実線の四角はプログラム,破線の四角は繰返しの処理,破線の四角から出る二つの矢印は分割を示す。

プログラム2の繰返しの処理を,スレッド2-1とスレッド2-2の二つに分割すると,cことがあるので,スレッド並列法を適用しない場合の実行結果と等しくなることを保証できない。したがって,プログラム2に対しては,繰返しの範囲の分割によるスレッド並列法を適用できない。
また,プログラム3の繰返しの処理を,スレッド3-1とスレッド3-2の二つに分割すると,dことがあるので,スレッド並列法を適用しない場合の実行結果と等しくなることを保証できない。したがって,プログラム3に対しても,繰返しの範囲の分割によるスレッド並列法を適用できない。

c に関する解答群
- a[51]の値をスレッド2-1で更新するより先にスレッド2-2で更新する
- a[51]の値をスレッド2-1で更新するより先にスレッド2-2で参照する
- a[51]の値をスレッド2-1で参照するより先にスレッド2-2で更新する
- a[51]の値をスレッド2-1で参照するより先にスレッド2-2で参照する
d に関する解答群
- a[51]の値をスレッド3-1で更新するより先にスレッド3-2で更新する
- a[51]の値をスレッド3-1で更新するより先にスレッド3-2で参照する
- a[51]の値をスレッド3-1で参照するより先にスレッド3-2で更新する
- a[51]の値をスレッド3-1で参照するより先にスレッド3-2で参照する
解答選択欄
- c:
- d:
- c=ウ
- d=イ
解説
〔cについて〕プログラム2は、
- a[1] ← a[2] + b[1]
- a[2] ← a[3] + b[2]
- a[3] ← a[4] + b[3]
・・・
次要素は更新処理前の値を参照する必要があるので、並列処理で、
- スレッド2-2側
- a[51] ← a[52] + b[51] //a[51]を更新
- スレッド2-1側
- a[50] ← a[51] + b[50] //更新後のa[51]を参照
したがって、2つのスレッドに分割したときに正しい結果が得られないのは、a[51] の値をスレッド2-1で参照するよりも先に、スレッド2-2で更新してしまった場合です。
∴c=ウ
また以下のように、a[51]を参照するのはスレッド2-1、更新するのはスレッド2-2であることに着目して正誤を判断することも可能です。
- スレッド2-1は i が1~50まで繰り返されるので、a[1]~a[50] の更新を行います。a[51] を更新するのはスレッド2-2です。
- 「ア」と同じ理由で誤りです。
- 正しい。
- スレッド2-2は i が51~100まで繰り返されるので、参照されるaの要素は a[52]~a[101] です。スレッド2-2で a[51] を参照することはありません。また、参照だけならばスレッド2-1の更新処理に影響を与えることはありません。
〔dについて〕
プログラム3は、
- a[2] ← a[1] + b[2]
- a[3] ← a[2] + b[3]
- a[4] ← a[3] + b[4]
・・・
前要素は更新した後の値を参照する必要があるので、並列処理で、
- スレッド3-2側
- a[52] ← a[51] + b[52] //更新前のa[51]を参照
- スレッド3-1側
- a[51] ← a[50] + b[51] //a[51]を更新
したがって、2つのスレッドに分割したときに正しい結果が得られないのは、a[51] の値をスレッド3-1で更新するよりも先に、スレッド3-2で参照してしまった場合です。
∴d=イ
また以下のように、a[51]を参照するのはスレッド3-2、更新するのはスレッド3-1であることに着目して正誤を判断することも可能です。
- スレッド3-2は i が52~101まで繰り返されるので、a[52]~a[101] の更新を行います。a[51]を更新するのはスレッド3-1なので誤りです。
- 正しい。
- 「ア」と同じ理由で誤りです。
- スレッド3-1は i が2~51まで繰り返されるので、参照されるaの要素は a[1]~a[50] です。スレッド3-1で a[51] を参照することはありません。
広告
設問3
図3に示すプログラム4では,配列 a における更新対象の位置を配列 ip の要素の値で指している。このプログラムでは,配列 ip の要素の値によって,スレッド並列法を適用できる場合とできない場合がある。
図4に示す配列 ip であれば,スレッド並列法を適用できる。図4中のeに入れる正しい答えを,解答群の中から選べ。
なお,図3において,実線の四角はプログラム,破線の四角は繰返しの処理,破線の四角から出る二つの矢印は分割を示す。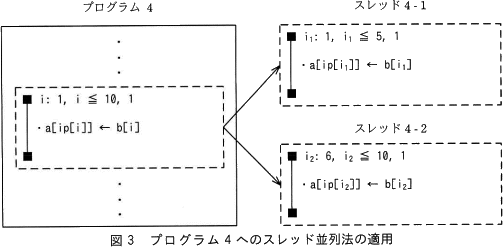
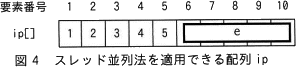
図4に示す配列 ip であれば,スレッド並列法を適用できる。図4中のeに入れる正しい答えを,解答群の中から選べ。
なお,図3において,実線の四角はプログラム,破線の四角は繰返しの処理,破線の四角から出る二つの矢印は分割を示す。


e に関する解答群
解答選択欄
- e:
- e=エ
解説
プログラム4は、配列ipで指定した位置の配列aを配列bの値で更新していく処理です。次のようなイメージを持ってもらえればいいと思います。
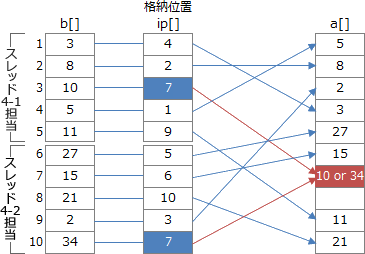
選択肢の中で1~5が含まれないのは「エ」だけです。
∴e=エ:

広告
広告