平成21年秋期試験午後問題 問1

問1 ハードウェア
半加算器と全加算器に関する次の記述を読んで,設問1~3に答えよ。
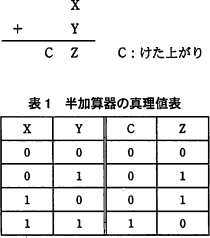
- 1ビット同士を加算する半加算器の真理値表を,表1に示す。
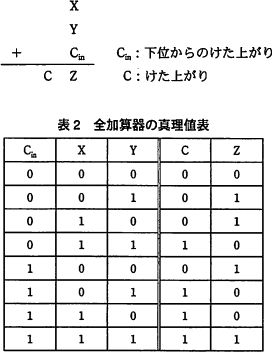
- 下位からのけた上がりCinを考慮して1ビット同士を加算する全加算器の真理値表を,表2に示す。
広告
設問1
半加算器を実現する論理回路を,図1に示す。図1中の に入れる正しい答えを,解答群の中から選べ。ただし,ANDは論理積,ORは論理和,XORは排他的論理和,NANDは否定論理積,NORは否定論理和を表す。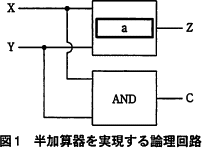

a に関する解答群
- AND
- NAND
- NOR
- OR
- XOR
解答選択欄
- a:
- a=オ
解説
半加算器(はんかさんき,Half adder)は、2進数の同じ桁どうしの演算をして(通常は最下位の桁)、桁上がりは桁上げ出力(Carry out)によって出力する回路です。に入る論理回路は、表1「半加算器を実現する論理回路」の入力X、YとZの関係に注目するとわかります。
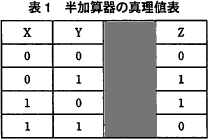
したがって、 に入る論理回路は、XORが適切です。
∴a=XOR
広告
設問2
全加算器を実現する論理回路について,次の記述中の に入れる正しい答えを,解答群の中から選べ。
全加算器は,図2に示すように半加算器を2段に接続して実現する。半加算器1はXとYを加算し,半加算器2は半加算器1の結果とCinを加算する。このとき,半加算器1のけた上がりをC1,半加算器2のけた上がりをC2 とする。X,Y,Cin と,C1,C2との関係は表3のとおりになる。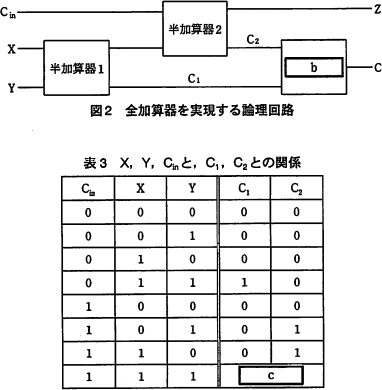
全加算器は,図2に示すように半加算器を2段に接続して実現する。半加算器1はXとYを加算し,半加算器2は半加算器1の結果とCinを加算する。このとき,半加算器1のけた上がりをC1,半加算器2のけた上がりをC2 とする。X,Y,Cin と,C1,C2との関係は表3のとおりになる。

b に関する解答群
- AND
- NAND
- NOR
- OR
c に関する解答群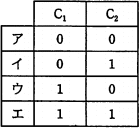

解答選択欄
- b:
- c:
- b=エ
- c=ウ
解説
全加算器(ぜんかさんき,Full adder)は、2進数の最下位以外の同じ桁どうしの演算をして、下位からの桁上げ入力を含めて出力する回路です。〔cについて〕
こちらから先に解いた方がわかりやすいので解説の順番を逆にします。
cにはいる3つの出力がすべて1(表の最下行)のときの、全加算器の途中にあるC1、C2の値を確認します。
まず半加算器1では、X、Yの演算が行われます。両方とも1なので繰上がり桁であるC1が1、Zが0になります。
半加算器2では、下位桁からの繰り上がりであるCinと半加算器1からのZ=0の演算が行われます。Cin=1、Z=0なので、繰上り桁であるC2は0、Zが1になります。
下図は回路図に出力値を書き入れたものです。
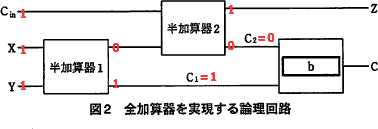
∴c=ウ:C1=1、C2=0
〔bについて〕
bに入る回路図を特定するためには、二つの入力C1、C2と最終的な出力Cの関係を確認する必要があります。
表2の「全加算器の真理値表」と表3「X、Y、Cinと、C1、C2の関係」を組み合わせたものが下表です。
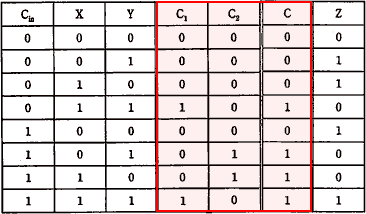
表を見ると、C1又はC2のどちらかが1であれば、出力Cには1が出力されるような関係になっていることがわかります。
この入出力の関係となる論理回路図はOR回路であるため、bに入るのはOR回路ということになります。
∴b=エ:OR
広告
設問3
A,B及びSを2の補数表現による4ビットの符号付2進整数とし,それぞれのビット表現をA4A3A2A1,B4B3B2B1,及びS4S3S2S1で表す(符号ビットはA4,B4及びS4)。
図3は,AとBの加算を行い,結果をSに求める加算器であり,半加算器と全加算器で実現されている。ここで,C1~C4は半加算器及び全加算器からのけた上がりを表す。
この加算器に,Aとして-1を,Bとして-2(いずれも10進表記)を与えたとき,図3のC1~C4の値として正しい組合せを,解答群の中から選べ。
図3は,AとBの加算を行い,結果をSに求める加算器であり,半加算器と全加算器で実現されている。ここで,C1~C4は半加算器及び全加算器からのけた上がりを表す。
この加算器に,Aとして-1を,Bとして-2(いずれも10進表記)を与えたとき,図3のC1~C4の値として正しい組合せを,解答群の中から選べ。

解答群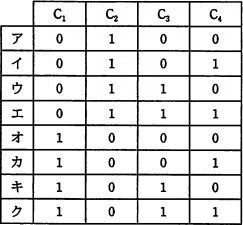

解答選択欄
- エ
解説
一見複雑に見える設問ですが、AとBを2の補数表現で表し地道に計算していくことで正解にたどりつくことができます。まず、A=-1とB=-2を2の補数表現に変換します。
先に変換方法を確認しておくと、絶対値がnである負数を2の補数表現で表す手順は、
- nを2進数で表す。
- すべてのビットを反転させる。
- 1を加算する。
手順通りにA、Bを変換すると、
- A=-1→0001→1110→1111
- B=-2→0010→1101→1110
これで、図3「AとBを加算してSを求める加算器」のA4A3A2A1、B4B3B2B1に入る値がわかったので、これを図に書き入れます。
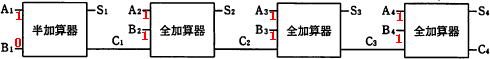

ちなみに演算結果を表すS4~S1の値は、1101となっており2の補数表現での"-3"を示しています。つまり、この加算器によって"-1+(-2)=-3"の演算が正しく行われたことがわかります。
∴エ:C1=0、C2=1、C3=1、C4=1
広告
広告