次の表計算及びワークシートの説明を読んで，設問1，2に答えよ。

〔表計算の説明〕
　ある企業では，アルバイトの勤務を管理するための勤怠管理表と出勤割当表の作成を手作業で行っていたが，これを表計算ソフトで行うことにした。

〔ワークシート：勤怠管理〕

• 表計算ソフトのワークシート"勤怠管理"を作成した。その例を図1に示す。
  
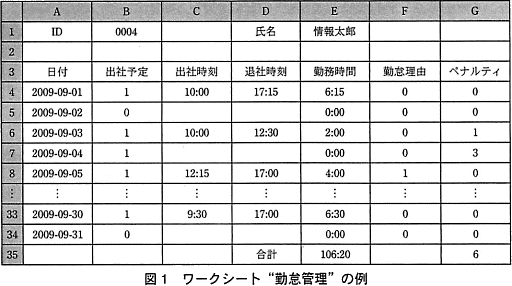
• 時刻及び時間の表記は h:mm，hh:mm 又は hhh:mm で表示されるが，内部では24時間を1とする実数値で記録されている。例えば，10:30は10.5／24＝0.4375，18:00は18／24＝0.75である。計算にはこの数値を利用する。
• 図1中の各項目の説明は，次のとおりである。
  

  ID，氏名

  アルバイトの識別番号と氏名である。

  日付：

  1か月分の日付が yyyy-mm-dd の形式で表示される。日数30日以下の月でも31日まで列挙する。

  出社予定：

  出社予定日には1を，出社予定でない日や2009-09-31のように存在しない日には0を格納する。

  出社時刻：

  始業時刻は10時である。10時に遅れた場合は遅刻扱いとなる。出社しなかった日，又は存在しない日のセルは空白とする。

  退社時刻：

  終業時刻は17時である。17時前の退社は早退扱いとなる。出社しなかった日，又は存在しない日のセルは空白とする。

  勤務時間：

  出社してから退社するまでの時間である。ただし，12時から13時までは昼休みであり，この時間は勤務時間に含まれない。出社しなかった日は0:00が表示される。また，日をまたいで勤務することはない。

  勤怠理由：

  初期値は0である。欠勤，遅刻，早退について正当な理由がある場合は1を設定する。

  ペナルティ：

  正当な理由なく出社予定日に欠勤した場合は3を，正当な理由なく遅刻又は早退した場合は1を表示する。これら以外の場合は0を表示する。

  合計(勤務時間)：

  当該月の勤務時間の合計を表示する。

  合計(ペナルティ)：

  当該月のペナルティの合計を表示する。

  　ペナルティの合計は，出勤割当表を作成するときに利用する。

ワークシート"勤怠管理"に関する次の記述中の　に入れる正しい答えを，解答群の中から選べ。

　各日のペナルティを算出するために，ワークシート"勤怠管理"のセル G4 には次の式を入力し，セル G5～G34 に複写する。
　　IF(F4＝1,0,IF(a,3,
　　　　　　　IF(b,1,0)))
　ペナルティの合計を算出するために，セル G35 には次の式を入力する。
　　合計(G4～G34)
　各日の勤務時間を算出するために，ワークシート"勤怠管理"のセル E4 には次の式を入力し，セル E5～E34 に複写する。算術演算のとき，空白セルは0として取り扱われる。
　　c
　勤務時間の合計を算出するために，セル E35 には次の式を入力する。
　　合計(E4～E34)

a に関する解答群

• 否定(論理積(B4＝0,C4＝''))
• 否定(論理積(B4＝1,C4＝''))
• 否定(論理和(B4＝0,C4＝''))
• 否定(論理和(B4＝1,C4＝''))
• 論理積(B4＝1,C4＝'')
• 論理和(B4＝1,C4＝'')

b に関する解答群

• 論理積(B4＝1,論理積(C4≦(10／24),D4≧(17／24)))
• 論理積(B4＝1,論理和(C4＞(10／24),D4＜(17／24)))
• 論理積(C4≦(10／24),D4≧(17／24))
• 論理和(B4＝1,論理積(C4≦(10／24),D4≧(17／24)))
• 論理和(B4＝1,論理和(C4＞(10／24),D4＜(17／24)))
• 論理和(C4＞(10／24),D4＜(17／24))

c に関する解答群

• D4－C4－1／24
• 最小(D4,12／24)－最小(C4,12／24)＋最大(D4,13／24)－最大(C4,13／24)
• 最小(D4,13／24)－最小(C4,12／24)－1／24
• 最小(D4,13／24)－最大(C4,12／24)－1／24
• 最大(D4,12／24)－最小(C4,12／24)＋最大(D4,13／24)－最小(C4,13／24)
• 最大(D4,13／24)－最小(C4,12／24)－1／24
• 最大(D4,13／24)－最大(C4,12／24)－1／24

〔ワークシート：勤務可能調査〕
　月末になると翌月の出勤割当表の作成に先立って，アルバイトの申告した勤務可能日に基づいて，ワークシート"勤務可能調査"を作成する。その例を図2に示す。ワークシート"勤務可能調査"では，勤務可能なことを1で，勤務不可能なことを0で表す。また，存在しない日は，全員が0となる。
　なお，アルバイトは15名とする。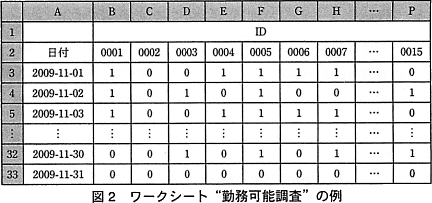〔ワークシート：出勤割当表〕

• ワークシート"勤務可能調査"に基づいて，ワークシート"出勤割当表"を作成する。その例を図3に示す。ワークシート"出勤割当表"では，勤務を割り当てた場合を1で，割り当てなかった場合を0で表す。
  
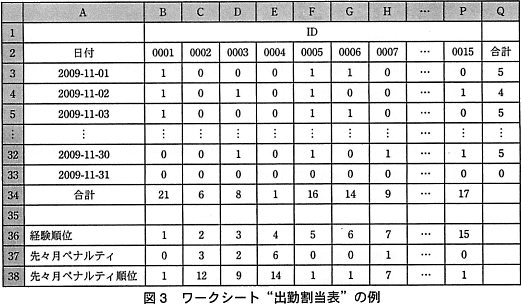
• 図3中の各項目の説明は，次のとおりである。

  経験順位：

  業務経験が長い人ほど小さい値が入力されている。同順位の人はいない。

  先々月ペナルティ：

  各アルバイトの先々月のペナルティの合計が入力されている。

  先々月ペナルティ順位：

  各アルバイトの先々月ペナルティを昇順に順位付けする。
  先々月ペナルティが同じ場合は同順位となる。

• 出勤割当表の作成は，月初から月末まで順番に1日分ずつ次の規則に基づいて行う。
  1. その日に出社可能な人が5人以下の場合は，その全員を割り当てる。
  2. その日に出社可能な人が5人より多い場合は，その中から次の優先順位で5人を割り当てる。
     1. 先々月ペナルティ順位がより小さい。
     2. ①が等しい場合は，既に割当てが決められた期間(月初から前日まで)に割り当てられた回数がより少ない。
     3. ①，②がともに等しい場合は，経験順位がより小さい。
• (3)の規則を定式化するために，出社の可否，先々月ペナルティ順位，前日までの割当回数，経験順位からなる次のような7けたの数値(以下，評価値という)を定義する。
  
  　この評価値が小さい人から，順番に出勤を割り当てる。評価値の計算には，ワークシート"出勤割当表"の列AB～APを使用する。
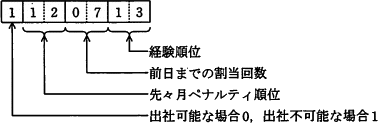
• ワークシート"出勤割当表"で用いる関数を表に示す。
  
• 複数のワークシート間でデータを参照する場合には，"ワークシート名!セル"又は"ワークシート名!セル範囲"という形式で指定する。

ワークシート"出勤割当表"に関する次の記述中の　に入れる正しい答えを，解答群の中から選べ。

　先々月ペナルティ順位を算出するために，ワークシート"出勤割当表"のセル B38 には次の式を入力し，セル C38～P38 に複写する。
　　順位(B37,$B37～$P37,0)
　次に，セル AB3～AP33 に評価値を設定する。
　セル AB3 には次の式を入力し，セルAC3～AP3に複写する。
　　(((1－勤務可能調査!B3)*100＋d)*100)*100＋e
　セル AB4 には次の式を入力し，セル AB4～AP33 に複写する。
　　(((1－勤務可能調査!B4)*100＋d)*100＋f)*100
　　＋e
　出勤者を決定するために，セルB3には次の式を入力し，セル B3～P33 に複写する。
　　IF(論理積(g，
　　　　　　　h),1,0)
　各アルバイトの割当日数の合計を算出するために，セル B34 には次の式を入力し，セル C34～P34 に複写する。
　　合計(B3～B33)
　各日の合計割当人数を算出するために，セル Q3 には次の式を入力し，セル Q4～Q33 に複写する。
　　合計(B3～P3)

d，e，f に関する解答群

• B$3
• B$36
• B$38
• B3
• B36
• B38
• 合計(B$3～B3)
• 合計(B$3～$B3)

g，h に関する解答群

• 勤務可能調査!B3＝0
• 勤務可能調査!B3＝1
• 合計($B3～$P3)≦5
• 合計($B3～$P3)≧5
• 合計(勤務可能調査!$B3～$P3)≦5
• 合計(勤務可能調査!$B3～$P3)≧5
• 順位(AB3,$AB3～$AP3,0)≦5
• 順位(AB3,$AB3～$AP3,1)≦5
• 順位(B3,$B3～$P3,0)≦5
• 順位(B3,$B3～$P3,1)≦5