平成21年春期試験午後問題 問1

問1 ハードウェア
画像データの符号化に関する次の記述を読んで,設問1~3に答えよ。
図1は,8×8画素の白と黒だけで色分けされた2値画像の例である。画素を1番上の行の左から右へ,次に2番目の行の左から右へと順に1画素を1ビットで,白を0,黒を1で表すと,図2のように64ビットのビット列で表現することができる。
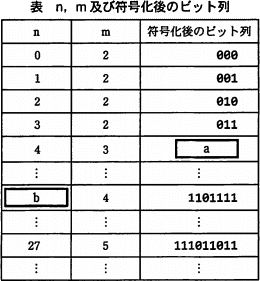
図1は,8×8画素の白と黒だけで色分けされた2値画像の例である。画素を1番上の行の左から右へ,次に2番目の行の左から右へと順に1画素を1ビットで,白を0,黒を1で表すと,図2のように64ビットのビット列で表現することができる。

- 図2のビット列を,同じ値が連続している部分(以下,ランという)ごとに区切り,各ランをその連続する個数(以下,ランレングスという)で表すことによって,少ないビット数でのビット列表現に書き換えることができる。図2では,左上から数えて0が27個,1が27個,0が10個の順に連続しているので,27,27,10という情報を使った表現に書き換える。これを,ランレングス符号化という。
- 1番上の行の左端の画素は白で始まるものとする。ただし,その画素が黒の場合は,先頭に0個の白があるものとして符号化を行う。
- ランレングス符号化の方法は,次のとおりである。
- ランレングスをnとし,nを2進数で表現したときのけた数をmとする。ただし,常にm≧2となるように,n=0の2進数表現を00,n=1の2進数表現を01とする。
- nビットのランを図3のビット列に書き換える。

- 図2の例では,最初は0が27個連続しているので,n=27である。27を2進数で表現すると11011(5けた)となり,m=5である。m-2=3なので,けた数情報は111である。 したがって,この部分の符号化後のビット列表現は111011011となり,9ビットで表現できる。
- 表にn,m及び符号化後のビット列を示す。

広告
設問1
表中の に入れる正しい答えを,解答群の中から選べ。
a に関する解答群
- 100
- 0100
- 10100
- 110100
b に関する解答群
- 14
- 15
- 16
- 17
解答選択欄
- a:
- b:
- a=ウ
- b=イ
解説
〔aについて〕設問の手順に従って符号化を行います。
- mは10進数のnを2進数に変換したときのけた数です。n=4は、
4(10)→100(2)
と変換されるので、m=3になります。 - m,nをランレングスのビット列に当てはめると、
- けた数情報は(m-2)個の連続する1です。3-2=1なので(a)の部分は1になります。
- 区切りは常に1個の0です。(b)は0になります。
- nの2進数表現が入ります。4(10)→100(2)なので(c)は100になります。
∴a=ウ:10100
〔bについて〕
符号化後のビット列の中で最初に現れる「0」は(b)区切りを表しています。つまりnを2進数にしたビット列が1111ということです。2進数1111を10進数に変換すると、
1111(2)=23+22+21+20
=8+4+2+1=15(10)
n=15とわかります。
∴b=イ:15
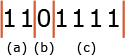
広告
設問2
図2の64ビットのビット列をランレングス符号化すると,何ビットで表現できるか。正しい答えを,解答群の中から選べ。
解答群
- 22
- 23
- 24
- 25
解答選択欄
- エ
解説
設問のビット列は 0:27個→1:27個→0:10個 で構成されているため、これらにランレングス符号化を施します。[0:27個]
n=27(10)→11011(2)
m=5
(a)の長さ=m-2=3
以上より(a)=111,(b)=0,(c)=11011
この部分のビット列は(a),(b),(c)を連結した「111011011」になるため、ビット数は9です。
[1:27個]
上記と同様に9ビットになります。
[0:10個]
n=10(10)→1010(2)
m=4
(a)の長さ=m-2=2
以上より(a)=11,(b)=0,(c)=1010
この部分のビット列は「1101010」になるため、ビット数は7です。
したがって3つの符号化ビット列の長さ(9,9,7)を足した25になります。
∴エ:25
広告
設問3
ランレングス符号化後のビット列が,次のとおりであったとする。このビット列を復号した2値画像として正しい答えを,解答群の中から選べ。
000111011111111011111010
000111011111111011111010
解答群
解答選択欄
- エ
解説
まずは与えられたビット列をランごとに分割しなければなりません。始めが「0」、すなわち区切りから開始するということは(a)の部分が存在しないm=2以下のランと判断できます。mが2以下の場合は常に符号化後のビット列長が2ビットになるため、0に続く2ビット「00」が(c)になります。
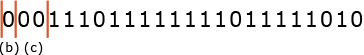
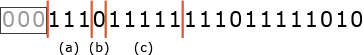
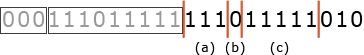
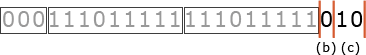
- 000
- 111011111
- 111011111
- 010
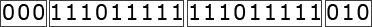
(c)=00
00(2)→0(10)個
設問中に「1番上の左端の画素は白で始まるものとする。ただし,その画素が黒の場合は、先頭に0個の白がある者として符号化を行う」という記述があるため、このランは0個の白に該当すると判断できます。
[111011111]
(c)=11111
11111(2)→31(10)個
●31個のランに変換されます。
[111011111]
(c)=11111
11111(2)→31(10)個
○31個のランに変換されます。
[010]
(c)=10
10(2)→2(10)個
●2個のランに変換されます。
以上より、画像の左上より●31個→○31個→●2個と並んでいる「エ」が正解と分かります。
広告
広告



