平成22年春期試験午後問題 問2

問2 ソフトウェア
コンパイラとは,プログラム言語で記述された原始プログラムを翻訳して目的プログラムを生成するためのソフトウェアである。コンパイラの処理過程において,構文解析は字句解析が出力する字句を読み込みながら構文木を生成し,その字句の列が文法で許されているかどうかを解析する。
広告
設問1
次の記述中の に入れる正しい答えを,解答群の中から選べ。
2項演算子から成る式の構文は,2分木で表現される。2分木から目的プログラムを生成するには,2分木を深さ優先で探索しながら,帰り掛けに節の演算子を評価する。式の構文木と探索順序の例を図に示す。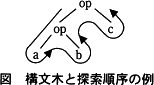 探索の結果,図の構文木の例は,aとbに対して演算opを施し,その結果とcに対して演算opを施すと解釈される。
探索の結果,図の構文木の例は,aとbに対して演算opを施し,その結果とcに対して演算opを施すと解釈される。
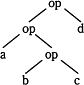
括弧を含む式では,演算の優先度は,括弧内の優先度が高く,それ以外は左から右に式を評価する。このとき,次の式に対する構文木は である。
式: a op (b op c) op d
2項演算子から成る式の構文は,2分木で表現される。2分木から目的プログラムを生成するには,2分木を深さ優先で探索しながら,帰り掛けに節の演算子を評価する。式の構文木と探索順序の例を図に示す。

括弧を含む式では,演算の優先度は,括弧内の優先度が高く,それ以外は左から右に式を評価する。このとき,次の式に対する構文木は である。
式: a op (b op c) op d
解答群
解答選択欄
- オ
解説
式: a op (b op c) op d の演算を考えると、まずbとcに対して演算opを施し、その結果とaに対して演算opを施し、さらにその結果とdに対して演算opを施すという順序になります。各選択肢の2分木を例と同じ方法で探索し、式が正しく解釈される木構造がどれかを確認していくことで正解がどれかを突き止めます。
木構造のデータを読み出す方法には三種類ありますが、例と同じ帰りがけ順/後行順序訪問で探索していきます。
帰りがけ順の探索では、
- ある節にたどり着いたら、その節の左の節のデータを読む。
もし、その節が部分木を持つのであれば1.を繰り返す - その節の右の節のデータを読む。
もし、その節が部分木を持つのであれば1を繰り返す - その節のデータを読む
- 親の節へ戻る
各木構造を帰りがけ順で探索・解釈していくと以下のようになります。
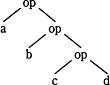
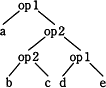
- cとdに演算opを施し、その結果とbに演算opを施す。さらにその結果とaに演算opを施すと解釈されます。
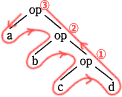
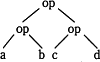
式で表すと、a op { b op (c op d)}となるので誤りです。 - aとbに演算opを施したものと、cとdに演算opを施したもの二つに対して演算opを施すと解釈されます。
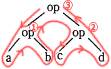
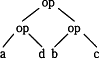
式で表すと、a op b op (c op d)となるので誤りです。 - aとdに演算opを施したものと、bとcに演算opを施したもの二つに対して演算opを施すと解釈されます。
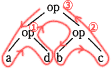
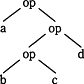
式で表すと、a op d op (b op c)となるので誤りです。< - bとcに演算opを施し、その結果とdに演算opを施す。さらにその結果とaに演算opを施すと解釈されます。
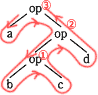
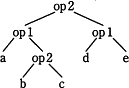
式で表すと、a op {(b op c) op d}となるので誤りです。 - bとcに演算opを施し、その結果とaに演算opを施す。さらにその結果とdに演算opを施すと解釈されます。
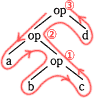
式で表すと、a op (b op c) op dとなるのでこれが正解となります。
広告
設問2
次の記述中の に入れる正しい答えを,解答群の中から選べ。
プログラム言語の文法は,構文規則で規定される。式の構文規則では式の構文を規定しているだけでなく,演算子の優先順位や結合規則も規定している。例として,優先順位が異なる演算子op1,op2と括弧を用いた式の構文規則を考える。
〔式の構文規則〕
式: a op1 b op2 c op2(d op1 e)
プログラム言語の文法は,構文規則で規定される。式の構文規則では式の構文を規定しているだけでなく,演算子の優先順位や結合規則も規定している。例として,優先順位が異なる演算子op1,op2と括弧を用いた式の構文規則を考える。
〔式の構文規則〕
- 式 → 項 | 式 op1 項
- 項 →因子 | 項 op2 因子
- 因子 → 名前 |(式)
- 名前 → a | b | c | d | e
"→"は,左側の構文要素が右側で定義されることを示す。
"|"は,"又は"を意味する。
式: a op1 b op2 c op2(d op1 e)
解答群
解答選択欄
- イ
解説
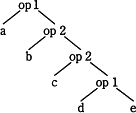
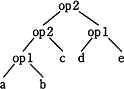
構文規則を規定する方法として疑似BNF記法が用いられており、この構文規則から正しい構文木が作成できるかが要点となります。〔式の構文規則〕に従いすべての要素を"名前"と"演算子"に分解していきます。この構文規則から構築された構文木は以下のようになります。
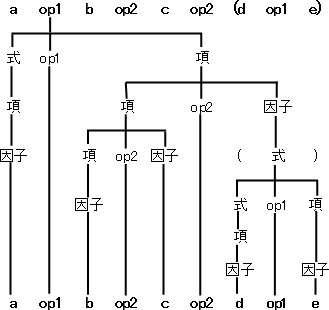
構文木作成のポイントは、b op2 c op2(d op1 e)の部分で、これを項を再帰的に解釈し(項 op2 因子) op2 因子と分解できるかどうかが、正しい2分木を描けるかの分かれ目になるのではないかと思います。
この木構造を見ると演算の優先度は、括弧つき"()"が最も高く、次いでop2、最後にop1が評価され最終的な式が構成されることがわかります。
広告
設問3
次の記述中の に入れる正しい答えを,解答群の中から選べ。
構文解析した結果は,構文木で表現する以外に,2分木と等価な表現の後置表記法(逆ポーランド表記法)で表現できる。後置表記法では,演算で使用する二つのオペランドを演算子の前に記述する。そして,後置表記法は,構文木を探索して得られる演算順序を表現したものであると考えることができる。例えば,設問1の図の例で,演算子opを加算+とした場合,後置表記法では ab+c+ となる。これは,aとbを加算し,その結果とcを加算することを表している。
後置表記法を用いて式 a×b+c×d+e を表現すると になる。ここで,加算+と乗算×は,それぞれ設問2の演算子op1とop2に対応し,演算の優先順位や結合規則は,〔式の構文規則〕に従うものとする。
構文解析した結果は,構文木で表現する以外に,2分木と等価な表現の後置表記法(逆ポーランド表記法)で表現できる。後置表記法では,演算で使用する二つのオペランドを演算子の前に記述する。そして,後置表記法は,構文木を探索して得られる演算順序を表現したものであると考えることができる。例えば,設問1の図の例で,演算子opを加算+とした場合,後置表記法では ab+c+ となる。これは,aとbを加算し,その結果とcを加算することを表している。
後置表記法を用いて式 a×b+c×d+e を表現すると になる。ここで,加算+と乗算×は,それぞれ設問2の演算子op1とop2に対応し,演算の優先順位や結合規則は,〔式の構文規則〕に従うものとする。
解答群
- abcd××+e+
- abc×+d×e+
- ab×cd×+e+
- ab×c+d×e+
解答選択欄
- ウ
解説
通常の式を後置表記法(=逆ポーランド表記法)逆ポーランド表記法に直すだけの単純な問題です。設問2にて演算の優先順位が把握できていれば、午前の小問を解いたことのある人ならいとも簡単に答えることができると思います。
演算の優先度は、括弧つき>op2(×)>op1(+)です。これを頭に入れて a×b+c×d+e を逆ポーランド表記法に変換してみましょう。
通常の式を、逆ポーランド表記法で表現するための基本は、A+BをAB+で表すことです。これと一回使った演算子は2度使わないことに注意して、普通に計算式を解くのと同じ要領で行っていくことで逆ポーランド表記法の式になります。
a×b+c×d+eを、1つずつ変換していきます。
- まず式の中で演算優先順位が高い a×b と c×d を変換します。a×bは"ab×"に、c×dは"cd×"になります。
a×b+c×d+e→ab×+cd×+e - 次にa×bの結果であるab×と、c×dの結果であるcd×を加算します。この時"ab×"や"cb×"を一つの項として考えると、現在どこを変換しているのかが理解しやすいかと思います。
ab×+cd×+e → ab×cd×++e - 最後にこれまでの演算結果であるab×cd×+に、eを加算します。
ab×cd×++e → ab×cd×+e+
a×b+c×d+eを逆ポーランド表記法で表現すると、ab×cd×+e+となるため答えは「ウ」が適切です。
広告
設問4
次の記述中の に入れる正しい答えを,解答群の中から選べ。
後置表記法で表現された式は,スタックを使って左から右に評価することができる。式 a+b+c×d を後置表記法に変換して評価する場合,スタックの操作順序は である。ここで,スタックを操作する命令として次の種類がある。また,加算+と乗算×は,それぞれ設問2の演算子op1とop2に対応し,演算の優先順位や結合規則は,〔式の構文規則〕に従うものとする。
後置表記法で表現された式は,スタックを使って左から右に評価することができる。式 a+b+c×d を後置表記法に変換して評価する場合,スタックの操作順序は である。ここで,スタックを操作する命令として次の種類がある。また,加算+と乗算×は,それぞれ設問2の演算子op1とop2に対応し,演算の優先順位や結合規則は,〔式の構文規則〕に従うものとする。
- push(x):
- スタックにxをプッシュする。

- add:
- スタックからオペランドを二つポップして加算し,その結果をスタックにプッシュする。
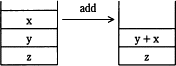
- mul:
- スタックからオペランドを二つポップして乗算し,その結果をスタックにプッシュする。
解答群
- push(a)→add→push(b)→add→push(c)→mul→push(d)
- push(a)→push(b)→add→push(c)→mul→push(d)→add
- push(a)→push(b)→add→push(c)→push(d)→mul→add
- push(a)→push(b)→push(c)→push(d)→add→add→mul
解答選択欄
- ウ
解説
まず式 a+b+c×d を後置表記法に変換します。設問3と同様の手順で変換を施すと、
a+b+c×d→a+b+cd×→ab++cd× → ab+cd×+
となり、ab+cd×+として表記されます。
式a+b+c×dを言葉にすると「aとbを加算したものと、cとdを乗算したものを足し合わせる」というように解釈ができると思います。
選択肢の中でこれを満たす操作順序を考えると、
- 通常の式そのままをスタック命令にしただけの順序です。スタックに一つしかオペランドが入っていない状態でadd命令をしていることなど誤りだらけであることがわかります。
- この順序だとaとbを加算したものとcを乗算し、その結果にdを足し合わせることになるため誤りです。
この順序が示す式は、(a+b)×c+dになります。 - 正しい。
- この順序だとbとcとdを加算した結果と、aを乗算することになるので誤りです。
この順序が示す式は、a×(b+c+d)になります。

広告
広告