平成22年春期試験午後問題 問4

問4 ネットワーク
動画のストリーミングサーバの設置計画に関する次の記述を読んで,設問1,2に答えよ。
S社は表1に示す要件で動画のストリーミングサーバ(以下,サーバという)の設置を計画している。
S社は表1に示す要件で動画のストリーミングサーバ(以下,サーバという)の設置を計画している。

広告
設問1
次の記述中の に入れる正しい答えを,解答群の中から選べ。
サーバに格納される動画のデータ量は約 aGバイトであり,サーバから動画を送信するときに要求されるビット速度は,平均でbMビット/秒である。ここで,1Gバイト=109バイト,1Mビット=106ビットとする。
サーバに格納される動画のデータ量は約 aGバイトであり,サーバから動画を送信するときに要求されるビット速度は,平均でbMビット/秒である。ここで,1Gバイト=109バイト,1Mビット=106ビットとする。
a に関する解答群
- 1.5
- 12
- 15
- 30
- 120
b に関する解答群
- 7.5
- 15
- 30
- 60
- 75
解答選択欄
- a:
- b:
- a=ウ
- b=ウ
解説
ストリーミング(streaming)とは、主に音声や動画などのマルチメディアファイルを転送・再生する方式の一種です。ファイルをダウンロードしながら、同時に再生をすることで、ユーザがファイルのダウンロード完了を待つことがなくなり、再生開始までの時間が短縮されるメリットがあります。〔aについて〕
表1「動画ストリーミングの要件」より、動画1本当たりのデータ量は、
0.5Mビット×240秒=120Mビット=15Mバイト
と計算され、サーバに格納される動画の本数は1000本なので、
15Mバイト×1000本=15Gバイト
したがってサーバに格納される動画のデータ量は、15Gバイトということになります。
∴a=ウ: 15
〔bについて〕
動画1本当たりの平均再生時間は4分、クライアントから1分間に平均15本の要求があることから、設置されるストリーミングサーバでは下図のように最大で60本の動画データを同時に送信することが求められます。
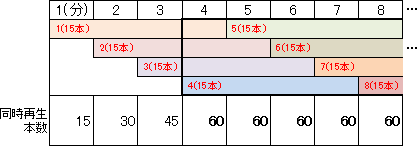
0.5Mビット×60=30Mビット
というように、平均で30Mビット/秒の送信速度が要求されることになります。
∴b=ウ: 30
広告
設問2
次の記述中の に入れる正しい答えを,解答群の中から選べ。
サーバは複数の動画を同時に送信可能である。また,クライアントからの要求はランダムに発生し,サーバが同時に送信可能な本数を上回る要求は待ち行列に入れられ,順次処理されるものとする。
このとき,クライアントの要求が待ち行列に入る確率Pは,待ち行列理論によって,二つの引数をとる関数fで計算することができる。引数の一つは,サーバが同時に送信可能な動画の本数nであり,もう一つは,要求されるトラフィックTである。この場合,Tは,cで,次の式で計算できる。
クライアントからの1分当たりの要求本数×動画1本の平均再生時間(分)
fを使いP,n,Tの関係を求めたものを,表2に示す。表2の網掛けの部分がTである。表2によれば,要件のとおり,要求が待たされる確率を10%以下にするためには,サーバが最低 d本の動画を同時に送信できなければならないことが分かる。
また,仮に,サーバが86本の動画を同時に送信できる能力をもつとき,要求が待たされる確率はおよそe%である。
なお,回線容量は十分にあり,通信の遅延はないものとする。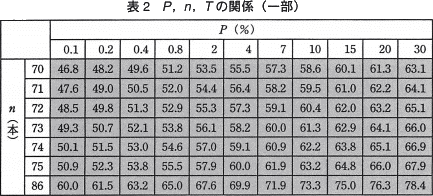
サーバは複数の動画を同時に送信可能である。また,クライアントからの要求はランダムに発生し,サーバが同時に送信可能な本数を上回る要求は待ち行列に入れられ,順次処理されるものとする。
このとき,クライアントの要求が待ち行列に入る確率Pは,待ち行列理論によって,二つの引数をとる関数fで計算することができる。引数の一つは,サーバが同時に送信可能な動画の本数nであり,もう一つは,要求されるトラフィックTである。この場合,Tは,cで,次の式で計算できる。
クライアントからの1分当たりの要求本数×動画1本の平均再生時間(分)
fを使いP,n,Tの関係を求めたものを,表2に示す。表2の網掛けの部分がTである。表2によれば,要件のとおり,要求が待たされる確率を10%以下にするためには,サーバが最低 d本の動画を同時に送信できなければならないことが分かる。
また,仮に,サーバが86本の動画を同時に送信できる能力をもつとき,要求が待たされる確率はおよそe%である。
なお,回線容量は十分にあり,通信の遅延はないものとする。

c に関する解答群
- 1分当たりに送信される動画の本数
- 1分当たりの動画の延べ再生時間
- ネットワーク帯域の最大占有率
- ネットワークの平均消費帯域幅
d に関する解答群
- 71
- 72
- 73
- 74
- 75
e に関する解答群
- 0.1
- 0.2
- 0.4
- 0.8
- 4
解答選択欄
- c:
- d:
- e:
- c=イ
- d=イ
- e=ア
解説
〔cについて〕問題文から、Tは要求されるトラフィックであり、
クライアントからの1分あたりの要求本数×動画1本当たりの平均再生時間(分)
で計算できることが分かっているので、4つの選択肢のうちからこの式で求められると考えられるものを選べばよいわけです。
上記の式に表1「動画ストリーミングサーバの要件」の数値を当てはめてみると、
15本×4分=60
となり、これは設問1の計算過程で現れたサーバが同時に送信することが要求される1分当たり60分の動画データ量と数値が一致することがわかります。
したがってTは、1分当たりの動画の延べ再生時間であることになります。
∴c=イ:1分当たりの動画の延べ再生時間
〔dについて〕
前問の式からT=60とわかっているので、これをもとに表2から空欄に該当する数値を求めます。
表2からT=60以上、要求が待たされる確率(P)が10%以下を満たす部分を色でわけると下図のようになります。(黄色:P≦10%を満たす範囲、青:T=60以上を満たす範囲、緑;二つの条件を満たす範囲)
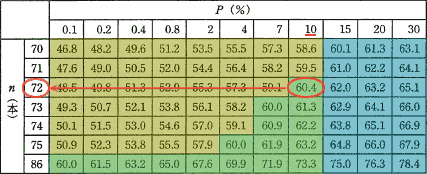
∴d=イ:72
〔eについて〕
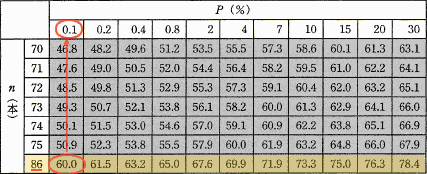
表より n=86本で、T=60の時に要求が待たされる確率(P)はおよそ0.1%になることがわかります。
広告
広告