平成23年秋期試験午後問題 問13

問13 ソフトウェア開発(表計算)
次の表計算,ワークシート及びマクロの説明を読んで,設問1,2に答えよ。
〔表計算の説明〕
三つの事業本部(以下,本部という)からなるK社では,次のルールに従って,社員の基本給及び賞与の額を決めている。
基本給計算の基となる役職ごとの役職給を登録した図1のワークシート"役職給"を作成した。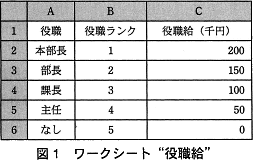 役職をセル A2~A6 に,役職の序列を示す数値である役職ランクをセル B2~B6 に,役職給をセル C2~C6 に入力する。
役職をセル A2~A6 に,役職の序列を示す数値である役職ランクをセル B2~B6 に,役職給をセル C2~C6 に入力する。
〔ワークシート:賞与係数〕
賞与の計算の基となる役職ごとの役職係数及び個人評価点に対応した個人評価係数を登録した図2のワークシート"賞与係数"を作成した。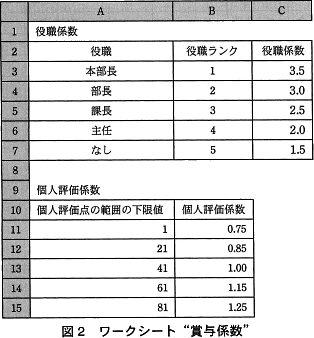
K社の三つの本部(第1本部,第2本部,第3本部)に所属する社員107名の基本給及び賞与を 計算するためのワークシート"基本給・賞与計算"を作成した。そのワークシートを図3に示す。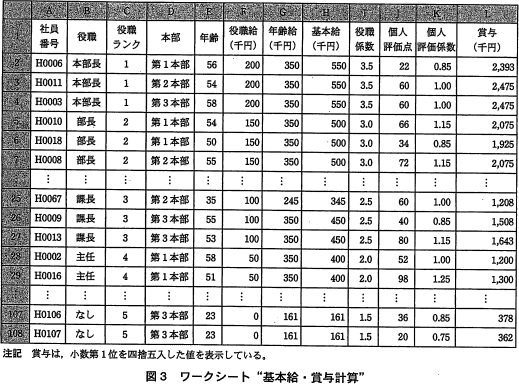
〔表計算の説明〕
三つの事業本部(以下,本部という)からなるK社では,次のルールに従って,社員の基本給及び賞与の額を決めている。
- 基本給
- 基本給は,毎月支給され,次の式で計算する。
基本給=年齢給+役職給 - 年齢給は,4月1日時点の年齢が50歳未満の場合,その年齢に7,000円を乗じて算出され,50歳以上の場合,固定額350,000円となる。
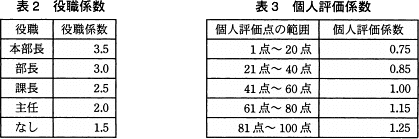
- 役職給の金額は,表1に示すとおりである。
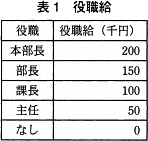
- 基本給は,毎月支給され,次の式で計算する。
- 賞与
- 賞与は,次の式で計算する。
賞与=基本給×(役職係数+個人評価係数) - 役職係数は,表2に示すとおりである。
- 個人評価係数は,表3に示すとおり個人評価点の範囲によって決まる。
- 賞与は,次の式で計算する。
基本給計算の基となる役職ごとの役職給を登録した図1のワークシート"役職給"を作成した。

〔ワークシート:賞与係数〕
賞与の計算の基となる役職ごとの役職係数及び個人評価点に対応した個人評価係数を登録した図2のワークシート"賞与係数"を作成した。

- 役職をセル A3~A7 に,役職ランクをセル B3~B7 に,役職係数をセル C3~C7 に入力する。
- 個人評価点の範囲の下限値をセル A11~A15 に,個人評価係数をセル B11~B15 に入力する。
K社の三つの本部(第1本部,第2本部,第3本部)に所属する社員107名の基本給及び賞与を 計算するためのワークシート"基本給・賞与計算"を作成した。そのワークシートを図3に示す。

広告
設問1
ワークシート"基本給・賞与計算"に関する次の記述中の に入れる正しい答えを,解答群の中から選べ。
- 社員番号をセル A2~A108 に,役職をセル B2~B108,本部をセル D2~D108 に,4月1日時点での年齢をセル E2~E108 に入力する。役職ランクを参照する計算式をセル C2~C108 に入力する。
- 基本給を求めるための計算式を入力する。
- 役職給を求める計算式aをセル F2 に入力し,セル F3~F108 に複写する。
- 年齢給を求める計算式bをセル G2 に入力し,セル G3~G108 に複写する。
- 基本給を求める計算式をセル H2~H108 に入力する。
- 賞与を求めるための計算式を入力する。
- 役職係数を求める計算式をセル I2~I108 に入力する。
- 個人評価点をセル J2~J108 に入力する。
- 個人評価点に対応した個人評価係数を求めるための計算式cをセル K2 に入力し,セル K3~K108 に複写する。
- 賞与を求める計算式をセル L2~L108 に入力する。
a に関する解答群
- 垂直照合(B1, 役職給!B$2~C$6, 2, 0)
- 垂直照合(B1, 役職給!B$2~C$6, 3, 0)
- 垂直照合(C2, 役職給!A$2~C$6, 2, 0)
- 垂直照合(C2, 役職給!B$2~C$6, 2, 0)
- 水平照合(B1, 役職給!B$2~C$6, 2, 0)
- 水平照合(B1, 役職給!B$2~C$6, 3, 0)
- 水平照合(C2, 役職給!A$2~C$6, 2, 0)
- 水平照合(C2, 役職給!B$2~C$6, 2, 0)
b に関する解答群
- IF(E2<49, C2*7, 350)
- IF(E2<49, E2*7, 350)
- IF(E2<50, C2*7, 350)
- IF(E2<50, E2*7, 350)
- IF(E2≦51, C2*7, 350)
- IF(E2≦51, E2*7, 350)
- IF(E2≧50, C2*7, 350)
- IF(E2≧50, E2*7, 350)
c に関する解答群
- 垂直照合(J2, 賞与係数!A$11~B$15, 2, 0)
- 垂直照合(J2, 賞与係数!A$11~B$15, 2, 1)
- 垂直照合(J2, 賞与係数!B$3~C$7, 2, 0)
- 垂直照合(J2, 賞与係数!B$3~C$7, 2, 1)
- 水平照合(J2, 賞与係数!A$11~B$15, 2, 0)
- 水平照合(J2, 賞与係数!A$11~B$15, 2, 1)
- 水平照合(J2, 賞与係数!B$3~C$7, 2, 0)
- 水平照合(G2, 賞与係数!B$3~C$7, 2, 1)
解答選択欄
- a:
- b:
- c:
- a=エ
- b=エ
- c=イ
解説
この設問の解説はまだありません。設問2
賞与の見直しに関する次の記述の に入れる正しい答えを,解答群の中から選べ。
K社では,役職及び個人評価に加えて,本部ごとの利益(以下,本部利益という)を賞与に反映するために,本部利益に応じた評価点(以下,本部加点という)を加味するよう賞与の計算式を見直すことにした。
〔見直した賞与計算方式に関する説明〕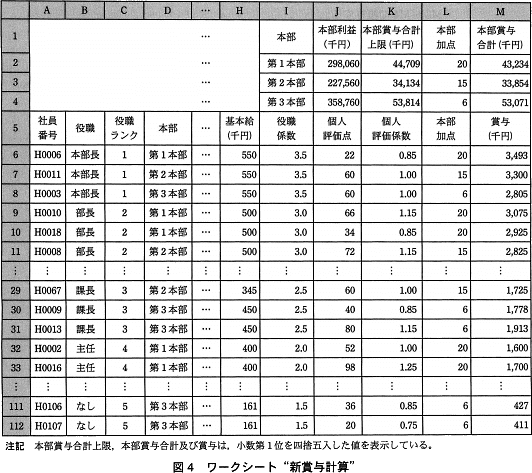 〔ワークシート:新賞与計算〕
〔ワークシート:新賞与計算〕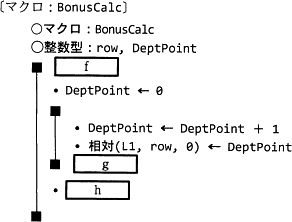
K社では,役職及び個人評価に加えて,本部ごとの利益(以下,本部利益という)を賞与に反映するために,本部利益に応じた評価点(以下,本部加点という)を加味するよう賞与の計算式を見直すことにした。
〔見直した賞与計算方式に関する説明〕
- 見直した賞与計算式は次のとおりである。
- 役職が本部長,部長又は課長のとき
賞与=基本給×(役職係数+個人評価係数+本部加点/10) - 役職が主任又はなしのとき
賞与=基本給×(役職係数+個人評価係数+本部加点/20)
- 役職が本部長,部長又は課長のとき
- 本部に属する社員の賞与の合計(以下,本部賞与合計という)が,本部利益の15%の金額(以下,本部賞与合計上限という)以下となる条件を満足する1~20の整数があるときは,その最大値を本部加点とする。無いときは,本部加点を0とする。

- 本部名をセル I2~I4 に,本部利益をセル J2~J4 に,本部賞与合計上限を求める計算式をセル K2~K4 に 入力する。
- ワークシート"基本給・賞与計算"のセル A1~K108 をワークシート"新賞与計算"のセル A5~K112 に複写する。
- 所属本部によって決まる社員ごとの本部加点を求める計算式をセル L6~L112 に入力する。社員ごとの賞与を求める計算式dをセル M6 に入力し,セル M7~M112 に複写する。
- 本部ごとの賞与合計を求める計算式eをセル M2 に入力し,セル M3~M4 に 複写する。
- マクロ BonusCalc は,各本部の条件を満足する本部加点を求めるマクロである。
- マクロ BonusCalc の処理手順は次のとおりである。
- 第1本部の本部加点の初期値を0とする。
- 本部加点に1を加算する。
- 手順②で設定された本部加点に基づき,第1本部に所属する社員の賞与の合計である第1本部の本部賞与合計をワークシートの計算式から算出する。
- 第1本部の本部賞与合計と本部賞与合計上限の値を比較し,前者が後者を上回る,又は,本部加点が20を超えたときは,手順⑤に進む。それ以外のときは,手順②に戻る。
- このときの本部加点から1を減じた値を第1本部の本部加点とし,対応するセルに代入する。
- 同様に,第2本部及び第3本部の本部加点をそれぞれ対応するセルに代入する。

d に関する解答群
- H6*(I6+K6)+IF(C6<3, L6/10, L6/20)
- H6*(I6+K6)+IF(C6<3, L6/20, L6/10)
- H6*(I6+K6)+IF(C6≦3, L6/10, L6/20)
- H6*(I6+K6)+IF(C6≦3, L6/20, L6/10)
- H6*(I6+K6+IF(C6<3, L6/10, L6/20))
- H6*(I6+K6+IF(C6<3, L6/20, L6/10))
- H6*(I6+K6+IF(C6≦3, L6/10, L6/20))
- H6*(I6+K6+IF(C6≦3, L6/20, L6/10))
e に関する解答群
- 条件付合計(C$6~C$112,=I2,L$6~L$112)
- 条件付合計(C$6~C$112,=I2,M$6~M$112)
- 条件付合計(D$6~D$112,=I2,L$6~L$112)
- 条件付合計(D$6~D$112,=I2,M$6~M$112)
- 照合検索(I2,C$6~C$112,L$6~L$112)
- 照合検索(I2,C$6~C$112,M$6~M$112)
- 照合検索(I2,D$6~D$112,L$6~L$112)
- 照合検索(I2,D$6~D$112,M$6~M$112)
f に関する解答群
- row: 1, row < 3, 1
- row: 1, row < 20, 1
- row: 1, row ≦ 3, 1
- row: 1, row ≦ 20, 1
- row: 2, row < 4, 1
- row: 2, row ≦ 4, 1
- row: 6, row < 112, 1
- row: 6, row ≦ 112, 1
g に関する解答群
- 論理積(M2≦K2,DeptPoint ≦20)
- 論理積(M2≦K2,L2≦20)
- 論理積(相対(L1,row,1)> 相対(L2,row,-1),DeptPoint >20)
- 論理積(相対(L1,row,1)≦ 相対(L1,row,-1),DeptPoint ≦20)
- 論理和(M2>K2,DeptPoint >20)
- 論理和(M2>K2,L2>20)
- 論理和(相対(L1,row,1)> 相対(L2,row,-1),DeptPoint >20)
h に関する解答群
- 相対(L1,row,0) ← DeptPoint
- 相対(L1,row,0) ← DeptPoint +1
- 相対(L1,row,0) ← DeptPoint -1
- 相対(L1,row,-1) ← DeptPoint
- 相対(L1,row,-1) ← DeptPoint +1
- 相対(L1,row,-1) ← DeptPoint -1
- 相対(L2,row,0) ← DeptPoint
- 相対(L2,row,0) ← DeptPoint +1
- 相対(L2,row,-1) ← DeptPoint +1
- 相対(L2,row,-1) ← DeptPoint -1
解答選択欄
- d:
- e:
- f:
- g:
- h:
- d=キ
- e=エ
- f=ウ
- g=エ
- h=ウ
解説
この設問の解説はまだありません。広告