平成24年春期試験午後問題 問8

問8 データ構造及びアルゴリズム
次のプログラムの説明及びプログラムを読んで,設問1~3に答えよ。
整数型関数 BitTest は,8ビットのデータ中の指定したビット位置にあるビットの値を検査して,結果を返す。整数型関数 BitCount は,8ビットのデータ中にある1のビットの個数を返す。
なお,本問において,演算子"&","|"は,二つの8ビット論理型データの対応するビット位置のビット同士について,それぞれ論理積,論理和を求め,8ビット論理型で結果を得るものとする。また,"~"Bという表記は,8ビット論理型定数を表す。
〔プログラム1の説明〕
整数型関数 BitTest を,次のとおりに宣言する。
○整数型関数:BitTest (8ビット論理型:Data,8ビット論理型:Mask)
検査される8ビットのデータは入力用の引数 Data に,検査をするビット位置の情報は入力用の引数 Mask に,それぞれ格納されている。Mask 中のビットの値が1であるビット位置に対応した Data 中のビットを検査して,次の返却値を返す。ここで,Mask 中には1のビットが1個以上あるものとする。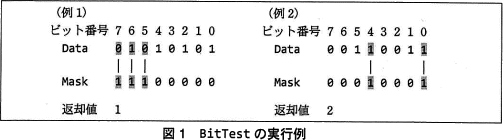
 〔プログラム2,3の説明〕
〔プログラム2,3の説明〕
整数型関数 BitCount を,次のとおりに宣言する。
○整数型関数:BitCount(8ビット論理型:Data)
検査される8ビットのデータは入力用の引数 Data に格納されている。
このためのプログラムとして,基本的なアルゴリズムを用いたプログラム2と,処理効率を重視したプログラム3を作成した。
プログラム2,3中の各行には,ある処理系を想定して,プログラムの各行を1回実行するときの処理量(1,2,…)を示してある。選択処理と繰返し処理の終端行の処理量は,それぞれの開始行の処理量に含まれるものとする。
なお,演算子"-"は,両オペランドを8ビット符号なし整数とみなして,減算を行うものとする。
整数型関数 BitTest は,8ビットのデータ中の指定したビット位置にあるビットの値を検査して,結果を返す。整数型関数 BitCount は,8ビットのデータ中にある1のビットの個数を返す。
なお,本問において,演算子"&","|"は,二つの8ビット論理型データの対応するビット位置のビット同士について,それぞれ論理積,論理和を求め,8ビット論理型で結果を得るものとする。また,"~"Bという表記は,8ビット論理型定数を表す。
〔プログラム1の説明〕
整数型関数 BitTest を,次のとおりに宣言する。
○整数型関数:BitTest (8ビット論理型:Data,8ビット論理型:Mask)
検査される8ビットのデータは入力用の引数 Data に,検査をするビット位置の情報は入力用の引数 Mask に,それぞれ格納されている。Mask 中のビットの値が1であるビット位置に対応した Data 中のビットを検査して,次の返却値を返す。ここで,Mask 中には1のビットが1個以上あるものとする。
- 返却値
- 0:検査した全てのビットが0
1:検査したビット中に0と1が混在
2:検査した全てのビットが1


整数型関数 BitCount を,次のとおりに宣言する。
○整数型関数:BitCount(8ビット論理型:Data)
検査される8ビットのデータは入力用の引数 Data に格納されている。
このためのプログラムとして,基本的なアルゴリズムを用いたプログラム2と,処理効率を重視したプログラム3を作成した。
プログラム2,3中の各行には,ある処理系を想定して,プログラムの各行を1回実行するときの処理量(1,2,…)を示してある。選択処理と繰返し処理の終端行の処理量は,それぞれの開始行の処理量に含まれるものとする。
なお,演算子"-"は,両オペランドを8ビット符号なし整数とみなして,減算を行うものとする。

広告
設問1
プログラム1中の に入れる正しい答えを,解答群の中から選べ。
a,b に関する解答群
- (Data & Mask) = "00000000"B
- (Data & Mask)= Data
- (Data & Mask) = Mask
- (Data | Mask) = "00000000"B
- (Data | Mask) = Mask
解答選択欄
- a:
- b:
- a=ウ
- b=ア
解説
プログラム1は、一般的なプログラム言語のif~else構文で表現する以下の構造になっています。if (a) {
RC ← 2
} else {
if (b) {
RC ← 0
} else {
RC ← 1
}
}
return RC
RCに代入される値より、このプログラムは以下のように動作することが読み取れます。RC ← 2
} else {
if (b) {
RC ← 0
} else {
RC ← 1
}
}
return RC
- 条件 a が真の場合
- 返却値が2:検査した全てのビットが1
- 条件 a が偽かつ条件 b が真の場合
- 返却値が0:検査した全てのビットが0
- 条件 a が偽かつ条件 b が偽の場合
- 返却値が1:検査したビット中に0と1が混在
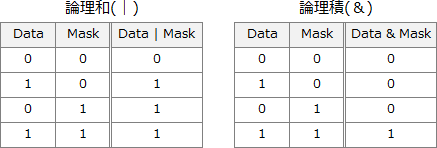
一方、論理積を求めた場合、Data 中のビットの値と演算結果の値が等しくなっています。
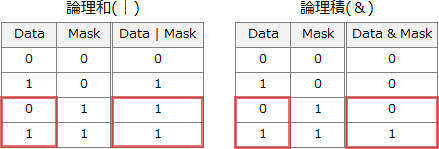
〔aについて〕
Data と Mask の論理積を求めた場合、論理積演算の性質により、検査対象でないビット(Mask 中で0であるビット)は必ず0になります。一方、検査対象のビット(Mask 中で1であるビット)は Data 中のビットの値がそのまま反映されます。
本条件式では「Data 中の検査対象のビットが全て1である」ことを判別します。検査対象ビットが全て1である場合、Data と Mask との論理積をとった結果は以下のようなビット列となります。
- Mask 中で0であるビット位置 ⇒ 0 & 0 = 0 又は 1 & 0 = 0(常に0)
- Mask 中で1であるビット位置 ⇒ 1 & 1 = 1(常に1)
∴a=ウ:(Data & Mask) = Mask
〔bについて〕
本条件式では「Data 中の検査対象のビットが全て0である」ことを判別します。この条件を満たす場合、Data と Mask の論理積は以下のようなビット列となります。
- Mask 中で0であるビット位置 ⇒ 0 & 0 = 0 又は 0 & 0 = 0(常に0)
- Mask 中で1であるビット位置 ⇒ 0 & 1 = 0(常に0)
∴b=ア:(Data & Mask) = "00000000"B
【別解】
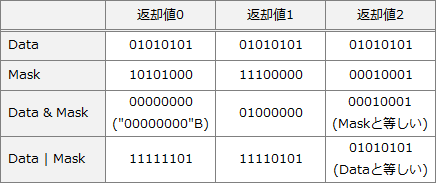
以下のように3種類それぞれの返却値が得られるデータパターンを考え、全パターンの論理積、論理和を一覧にしたうえで答えを求めることもできます。
[a]については2通りの答えが考えられますが、(Data | Mask) = Data は選択肢に存在しないため、「ウ」の (Data & Mask) = Mask が答えであることがわかります。
広告
設問2
次の記述中の に入れる正しい答えを,解答群の中から選べ。
プログラム1は,Mask 中に1のビットが1個以上あることを前提としている。ここで,この前提を取り除いて,Mask 中の1のビットが0個の場合は返却値0を返すようにしたい。そのために,プログラム1の処理部分について,次の修正案①~③を考えた。ここで,修正案①は,プログラム1のままで何も変更しない。また,aとbには,設問1の正しい答えが入っているものとする。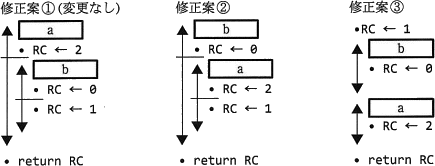 これらの修正案のうち,正しく動作するのはcである。
これらの修正案のうち,正しく動作するのはcである。
プログラム1は,Mask 中に1のビットが1個以上あることを前提としている。ここで,この前提を取り除いて,Mask 中の1のビットが0個の場合は返却値0を返すようにしたい。そのために,プログラム1の処理部分について,次の修正案①~③を考えた。ここで,修正案①は,プログラム1のままで何も変更しない。また,aとbには,設問1の正しい答えが入っているものとする。

c に関する解答群
- 修正案①
- 修正案②
- 修正案③
- 修正案①及び②
- 修正案①及び③
- 修正案②及び③
解答選択欄
- c:
- c=イ
解説
〔cについて〕関数 BitTest の修正に関する問題です。
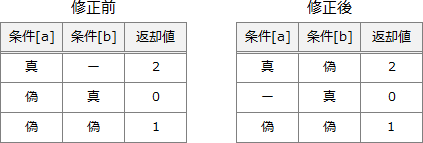
「Mask 中の1のビットが0個の場合は返却値0を返すようにしたい」とあるので、Mask = "00000000"B として、それぞれの修正案をトレースします。Data については適当な値で構いませんが、ここでは Data = "10101010"B とします。また、Mask 中の1のビットが1個以上ある場合に正しく動作する(修正前の動作が失われていない)ことも確認する必要があります。
【修正案①】
初めに分岐条件[a]の判定を行うと、(Data & Mask) = "00000000"B となります。(Data & Mask) = Mask であることから、[a]が真となります。これにより、Maskのビットが全て0であるにもかかわらず返却値は2となってしまい、設問の条件を満たしません。
したがって、修正案①は正しく動作しません。
【修正案②】
分岐条件[b]が先に判定されるようになっています。(Data & Mask) = "00000000"B となるため、[b]は真となります。これにより、返却値は0となり設問の条件を満たします。
なお、Mask 中の1のビットが1個以上ある場合も下図のように分岐し、正しく動作します。条件判定の"-"は判定が行われないことを表しています。
修正案①、②では1つ目の条件が偽の場合のみ、2つ目の条件が判定されていましたが、修正案③では1つ目の条件の真偽にかかわらず、2つ目の条件が判定されます。
修正案①、②でトレースしたように、条件[a]は真、条件[b]も真となるので、修正案③は以下のように動作します。
- RC に1が代入される
- 条件[b]を判定 ⇒ 真
- RC に0が代入される
- 条件[a]を判定 ⇒ 真
- RC に2が代入される
- RC を返却する
したがって、修正案③は正しく動作しません。
以上のトレース結果より、正しく動作するのは修正案②であるとわかります。したがって、[c]には「修正案②」が当てはまります。
∴c=イ:修正案②
広告
設問3
次の記述中の に入れる正しい答えを,解答群の中から選べ。
プログラム2,3の処理効率について考えてみる。表1にプログラム2,3の処理量の比較結果を示す。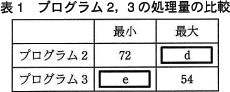 プログラム3では,αの行での変数 Work の更新において効率の良いアルゴリズムが使われている。例えば,プログラム3で引数 Data の内容が "01101010"B であったとき,繰返し処理においてαの行の2回目の実行が終了した時点で変数 Work の内容は,"f"Bになっている。このようなビット変換の処理によって,繰返し処理の繰返し回数は,検査されるデータ中の1のビットの個数と同じになる。
プログラム3では,αの行での変数 Work の更新において効率の良いアルゴリズムが使われている。例えば,プログラム3で引数 Data の内容が "01101010"B であったとき,繰返し処理においてαの行の2回目の実行が終了した時点で変数 Work の内容は,"f"Bになっている。このようなビット変換の処理によって,繰返し処理の繰返し回数は,検査されるデータ中の1のビットの個数と同じになる。
プログラム2,3の処理効率について考えてみる。表1にプログラム2,3の処理量の比較結果を示す。

d に関する解答群
- 80
- 88
- 104
- 112
e に関する解答群
- 6
- 10
- 20
- 22
f に関する解答群
- 00000011
- 00000110
- 00001010
- 01010000
- 01100000
- 10100000
解答選択欄
- d:
- e:
- f:
- d=ア
- e=ア
- f=オ
解説
解説の便宜上、プログラム2、3の各行について以下の番号(丸付き数字)を付けて解説します。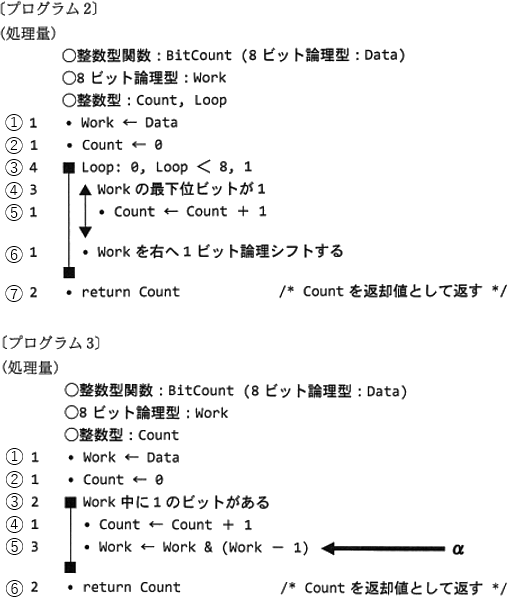
プログラム2は、①Data の最下位ビットが1であるかどうかを調べる、②Dataを右へ1ビット論理シフトする、という操作を8回繰り返すことで、Dataに含まれるビット"1"の数を調べています。処理量が最大となるのは全ビットが1で、④の処理が漏れなく実行される場合です。
各行が何回実行されるかを以下のことに注意してカウントし、合計します。
- ①②⑦は常に1回だけ実行されます。
⇒ 1+1+2=4 - ③はループ内処理が実行される8回に、ループを抜けるときの判定1回を加えて計9回実行されます。
⇒ 4×9=36 - ④⑥はループ内処理が実行される回数と同じ8回実行されます。
⇒ (3+1)×8=32 - ⑤は Data 中のビット"1"の数だけ実行されます。
⇒ 全ビットが1であれば、1×8=8
4+36+32+8=80
したがって[d]には「80」が当てはまります。なお、最小の72は、全ビットが0であるときに⑤が1回も実行されなかったときの処理量です。
【別解】
設問にプログラム2の最小処理量が既に72と記載されています。
処理量の違いは⑤の実行回数にのみ影響されること、⑤の実行回数は最小で0、最大で8であることから、プログラム2の最大処理量を「72+8=80」と求めることもできます。
∴d=ア:80
〔eについて〕
プログラム3では、③の繰り返し条件が「Work 中に1のビットがある」の前判定型になっていることから、処理量が最小となるのは Data = "00000000"Bの場合であると判断できます。この場合、繰り返し処理の内部(行④⑤)は実行されず、行①②③⑥が1回ずつ実行されてプログラムが終了します。
よって、以下の合計がプログラム3の最小処理量となります。
1+1+2+2=6
したがって[e]には「6」が当てはまります。
∴e=ア:6
〔fについて〕
プログラム3のトレースを行い、変数 Work の値を答える問題です。
問題文に従って、Data = "01101010"B としてプログラムの流れをトレースしていきます。なお、変数 Count の値は処理に影響しないため、Count に関する処理は省略しています。
⑤の処理が難しいため、最初に抜き出して解説しておきます。
まずは、(Work - 1)の部分から計算します。問題文中に「なお、演算子"-"は、両オペランドを8ビット符号なし整数とみなして、減算を行うものとする」とあります。1は8ビット符号なし整数に変換すると、00000001となります。よって、01101010 - 00000001という2進数の減算(引き算)を行います。以上より、(Work - 1) = "01101001"B となります。この時点では変数 Work の値自身は変化していないことに注意してください。
次に Work & (Work - 1)の計算を行います。
Work = "01101010"B、(Work - 1) = "01101001"B のため、これらの論理積を求めると、"01101000"B となります。
最後に計算結果を変数 Work に代入します。
まとめると、⑤の処理によって、変数 Work の値が "01101010"B から "01101000"B に変化しました。処理内容は分かりづらいですが、簡単に言ってしまえば、⑤の処理は「Work 中の1のうち、最も最下位(右側)にある1を0に書き換える処理」ということになります。
これらを踏まえて、プログラム3をトレースしていきます。
- ①:Work に Data の値を代入します。処理終了時点の Work = "01101010"B です。
- ③:Work = "01101010"B のため、「Work の中に1のビットがある」は真です。Work の値は変化しません。
- ⑤:Work の値が "01101010"B から "01101000"B に変化します。αの行の1回目の実行です。
- ループの終了行に達するため、開始行(行③)に戻ります。
- ③:Work = "01101000"B のため、「Work の中に1のビットがある」は真です。Work の値は変化しません。
- ⑤:Work の値が "01101000"B から "01100000"B に変化します。αの行の2回目の実行です。
∴f=オ:01100000
広告
広告