平成25年秋期試験問題 午前問75

問75解説へ
製品X及びYを生産するために2種類の原料A,Bが必要である。製品1個の生産に必要となる原料の量と調達可能量は表に示すとおりである。製品XとYの1個当たりの販売利益が,それぞれ100円,150円であるとき,最大利益は何円か。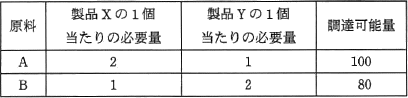

- 5,000
- 6,000
- 7,000
- 8,000
正解 ウ問題へ
広告
解説
線型計画法の考え方に従うと最大利益となる可能性のある生産方針は、以下のの3つのどれかになります。
- 製品Xを優先的に限界量まで生産
- 製品Yを優先的に限界量まで生産
- 調達可能量を全て使いきる製品XとYの組合せで生産
- 原料の調達可能量の制約からXの最大生産量は50個になります。Xの1個当たりの販売利益は100円なので、得られる利益は5,000円です。
- 原料の調達可能量の制約からYの最大生産量は40個になります。Yの1個当たりの販売利益は150円なので、得られる利益は6,000円です。
- 原料A、Bの両方を調達可能量まで使いきるときの、XとYの生産量の組合せを連立方程式で求めます。
{2X+Y=100 …①
{X+2Y=80 …②
①の式を変形
Y=100-2X …③
③の式を②の式に代入してXを求める
X+2(100-2X)=80
X+200-4X=80
-3X=120
X=40 …④
④の式を②の式に代入してYを求める。
40+2Y=80
2Y=40
Y=20
調達可能量まで原料A・Bを使った場合、Xを40個、Yを20個を生産することができます。このときに得られる利益は「100円×40個+150円×20個=7,000円」です。
広告