平成26年秋期試験午後問題 問2

問2 ハードウェア
JKフリップフロップに関する次の記述を読んで,設問1~3に答えよ。
JKフリップフロップは,二つの信号入力端子 J と K,一つのクロック信号入力端子 CLK,及び二つの信号出力端子 Q と Q をもつ回路である。図1にJKフリップフロップの記号を示す。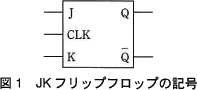 入出力される信号の値は高,低の二つの電圧レベルのいずれかである。クロック信号の値は,周期的に高と低を繰り返す。Q の値は,Q の値が高であれば低,低であれば高となる。
入出力される信号の値は高,低の二つの電圧レベルのいずれかである。クロック信号の値は,周期的に高と低を繰り返す。Q の値は,Q の値が高であれば低,低であれば高となる。
各入出力端子の信号の値を当該端子記号で表し,信号の値が高の場合を論理値の 1,低の場合を論理値の 0 として表記する。また,信号の値が低から高に変化することを 0→1,高から低に変化することを 1→0 と表記する。
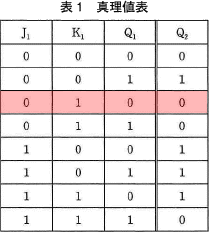
CLKの立ち下がり(1→0)時に,その時点でのJ,K,Qの値に基づき,その後のQの値が決定される。この様子を図2に示す。CLKの立ち下がり時刻をt1,その後のQの値が決定した時刻をt2として,時刻t1でのJ,K,Qの値(J1,K1,Q1と表記)と時刻t2のQの値(Q2と表記)の関係を表1の真理値表に示す。ここで,時刻t1とt2の時間間隔は極めて短く,CLK の1周期に比べても十分に短いものとする。
JKフリップフロップは,二つの信号入力端子 J と K,一つのクロック信号入力端子 CLK,及び二つの信号出力端子 Q と Q をもつ回路である。図1にJKフリップフロップの記号を示す。

各入出力端子の信号の値を当該端子記号で表し,信号の値が高の場合を論理値の 1,低の場合を論理値の 0 として表記する。また,信号の値が低から高に変化することを 0→1,高から低に変化することを 1→0 と表記する。
CLKの立ち下がり(1→0)時に,その時点でのJ,K,Qの値に基づき,その後のQの値が決定される。この様子を図2に示す。CLKの立ち下がり時刻をt1,その後のQの値が決定した時刻をt2として,時刻t1でのJ,K,Qの値(J1,K1,Q1と表記)と時刻t2のQの値(Q2と表記)の関係を表1の真理値表に示す。ここで,時刻t1とt2の時間間隔は極めて短く,CLK の1周期に比べても十分に短いものとする。

広告
設問1
次の記述中の に入れる正しい答えを,解答群の中から選べ。
図3に示すとおり,JとQ,KとQを それぞれ同一の値の信号とする回路(端子間を結線する)にクロック信号(CLK)を入力したとき,CLKの立ち下がりでQの値はa。ここで,Qの初期値は0とする。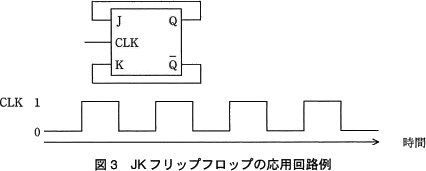
図3に示すとおり,JとQ,KとQを それぞれ同一の値の信号とする回路(端子間を結線する)にクロック信号(CLK)を入力したとき,CLKの立ち下がりでQの値はa。ここで,Qの初期値は0とする。

a に関する解答群
- 0のままである
- 0→1と変化する
- 0→1,1→0と変化する
- 0→1,1→0の変化を繰り返す
解答選択欄
- a:
- a=ア
解説
Qの初期値が 0 で、Qは 1 です。なので、Qに結線されたJも0、Qに結線されたKの値は1になります。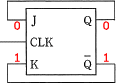
広告
設問2
表1の真理値表を基に,Q1からQ2への変化に着目し,そのときのJ1,K1との関係を表2にまとめ直した。表2中の に入れる正しい答えを,解答群の中から選べ。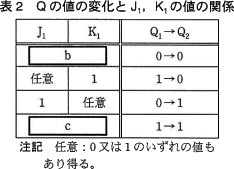

b,c に関する解答群
解答選択欄
- b:
- c:
- b=ア
- c=エ
解説
表1の真理値表を「0→0」「1→0」「0→1」「1→1」というQの4つの状態ごとにグループ化すると、次のようになります。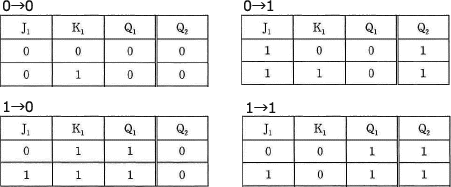
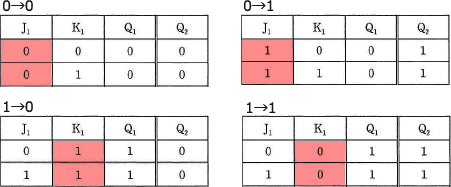
∴b=ア
c=エ
広告
設問3
JKフリップフロップ1個を使って,図4のように動作する2進カウンタを構成する。ここで,2進カウンタとは,CLKの1周期ごとにQの値が変化するものである。次の記述中の 入れる正しい答えを,解答群の中から選べ。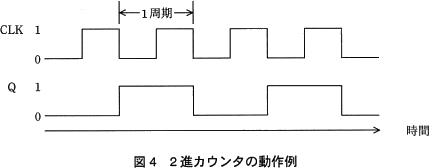 図4の例では,Qの値は,1回目のCLKの立ち下がりで0→1,2回目のCLKの立ち下がりで1→0に変化し,以降もCLKの立ち下がりごとにこれを繰り返す。
図4の例では,Qの値は,1回目のCLKの立ち下がりで0→1,2回目のCLKの立ち下がりで1→0に変化し,以降もCLKの立ち下がりごとにこれを繰り返す。
表2から,1回目のCLKの立ち下がりのときのJ,K,Qの値の組合せと,2回目のCLKの立ち下がりのときのJ,K,Qの値の組合せが,表3のようであればよいことが分かる。 例えば,表3の任意Jの値を0,任意Kの値を1にするためには,QをJの入力に,Kの入力の値を常に1にすればよい。(以下,(J,K)=(Q,1)と 表記する)この構成例を図5に示す。
例えば,表3の任意Jの値を0,任意Kの値を1にするためには,QをJの入力に,Kの入力の値を常に1にすればよい。(以下,(J,K)=(Q,1)と 表記する)この構成例を図5に示す。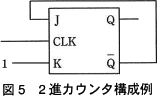 同様に,表3の任意Jと任意Kを組み合わせると,他の構成案として次の三つがある。
同様に,表3の任意Jと任意Kを組み合わせると,他の構成案として次の三つがある。
2進カウンタ構成案1 (J,K)=(d)
2進カウンタ構成案2 (J,K)=(e)
2進カウンタ構成案3 (J,K)=(f)

表2から,1回目のCLKの立ち下がりのときのJ,K,Qの値の組合せと,2回目のCLKの立ち下がりのときのJ,K,Qの値の組合せが,表3のようであればよいことが分かる。


2進カウンタ構成案1 (J,K)=(d)
2進カウンタ構成案2 (J,K)=(e)
2進カウンタ構成案3 (J,K)=(f)
d,e,f に関する解答群
- 1,1
- 1,Q
- 1,Q
- Q,1
- Q,Q
- Q,Q
解答選択欄
- d:
- e:
- f:
- d=ア
- e=イ
- f=カ
解説
表3 CLKの立ち下がりのときのJ,K,Qの組合せを満たすためには、1回目のCLK立ち下がり時にJ=1,2回目のCLK立ち下がり時にはK=1であることが求められます。各選択肢の(J,K)を設定した場合に、それぞれのCLK立ち下がり時のビットの状態がどうなるかの全パターンを列挙すると次のようになります。1回目のCLK立ち下がり時にJ=1,2回目のCLK立ち下がり時にはK=1である組合せが有効な構成案ということになります。
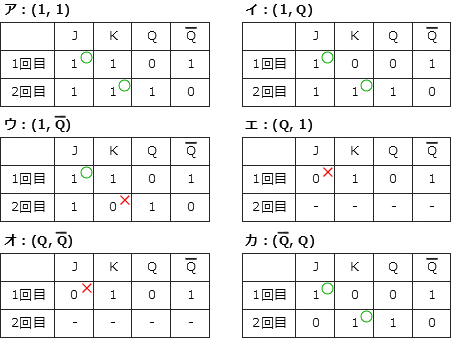
∴ア,イ,カ
広告
広告




