平成26年秋期試験午後問題　問8

午前試験免除制度対応！基本情報技術者試験のeラーニング【独習ゼミ】

問8　データ構造及びアルゴリズム

次のプログラムの説明及びプログラムを読んで，設問1，2に答えよ。

　二つの文字列の差異を測る指標に編集距離がある。編集距離の概念は，文書比較や検索キーワードの候補の提示などに用いられている。編集距離とは，1文字の追加操作又は削除操作を繰り返し適用し，ある文字列を別の文字列に変換するのに必要な最小の操作回数である。例えば文字列"abcabba"を文字列"cbabac"に変換する場合，図1に示す操作1～5によって変換が完了する。図1は，最小の操作回数で変換する一例を示しており，編集距離は5となる。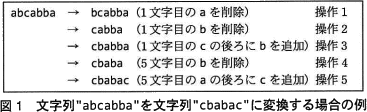
pm08_1.png
　関数 CalcEditDistance は，二つの文字列間の編集距離を返す関数である。
  • 変換元の文字列をStr1[]，変換先の文字列をStr2[]とする。また，配列の添字は0から始まり，文字列Str1[]のi番目の文字はStr1[i－1]と表記する。したがって，Str1[]＝"abcabba"の場合，1番目の文字＝Str1[0]＝"a"，2番目の文字＝Str1[1]＝"b" となる。Str2[]についても同様である。
  • 関数 CalcEditDistance は，エディットグラフと呼ばれるグラフの最短距離取得問題の考え方に基づいて，編集距離を求めている。編集距離の求め方は次のとおりである。
    1. 次の手順で，xy平面上にエディットグラフを作成する。ここで，Str1Len はStr1[]の文字数，Str2Len はStr2[]の文字数である。
      1. 0≦X≦Str1Len を満たす全ての整数Xに対して，点(X，0)から点(X，Str2Len)に線分を引く。
      2. 0≦Y≦Str2Len を満たす全ての整数Yに対して，点(0，Y)から点(Str1Len，Y)に線分を引く。
      3. 0≦X＜Str1Len，0≦Y＜Str2Len を満たす全ての整数X，Yの組に対して，Str1[X]とStr2[Y]が同一の文字の場合，点(X，Y)から点(X＋1，Y＋1)に線分を引く。
    2. エディットグラフを構成する線分をたどって，点(0，0)から点(Str1Len，Str2Len)へ移動する経路を考える。点(X，Y)から点(X＋1，Y)又は点(X，Y＋1)への移動距離を1，点(X，Y)から点(X＋1，Y＋1)への移動距離を0としたときの，点(0，0)から点(Str1Len，Str2Len)までの最短移動距離が編集距離となる。
  • Str1[]="abcabba"，str2[]="cbabac" の場合のエディットグラフを図2の左に示す。この場合に，最短移動距離となる経路の一つを図2の右に→で示す。
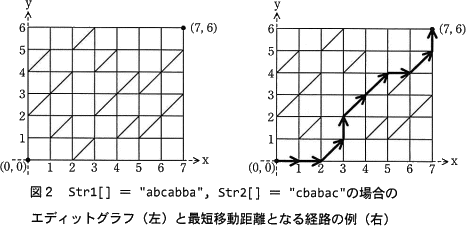
    pm08_2.png
  • 関数 CalcEditDistance では，点(0，0)から点(X，Y)への最短移動距離をD[X，Y]に求めている。D[X，Y]は，既に算出されているD[X－1，Y－1]，D[X，Y－1]，D[X－1，Y]を用いて求めることができる。これによって編集距離を算出している。
　〔関数 CalcEditDistance の引数と返却値〕
　関数 CalcEditDistance の引数の仕様は，次のとおりである。各配列の添字は，0から始まる。
pm08_3.png
　関数 CalcEditDistance では，次の関数 Min を使用している。

〔関数 Min の仕様〕
　引数として与えられた二つ以上の整数値の中で最も小さい値を返却値とする。
pm08_4.png
広告

設問1

プログラム中の　に入れる正しい答えを，解答群の中から選べ。
a に関する解答群
  • Str1[X－1] ＝ Str2[Y－1]
  • Str1[X－1] ≠ Str2[Y－1]
  • Str1[X] ＝ Str2[Y]
  • Str1[X] ≠ Str2[Y]
  • Str1[X－1] ＝ Str1[X] and Str2[Y－1] ＝ Str2[Y]
  • Str1[X－1] ≠ Str1[X] and Str2[Y－1] ≠ Str2[Y]
b に関する解答群
  • D[0，Str2Len]
  • D[Str1Len，0]
  • D[Str1Len，Str2Len]
  • D[Str1Len，Str2Len]＋1
  • D[Str1Len－1，Str2Len－1]
  • D[Str1Len－1，Str2Len－1]＋1
解答選択欄
  • a:
  • b:
  • a=ア
  • b=ウ

解説

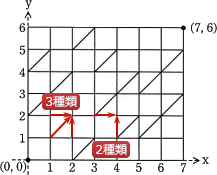
〔aについて〕
問題文より D[X，Y] は点(0，0)から点(X，Y)への最短移動距離であることがわかります。点(X, Y)への最短移動距離は、点(X, Y)へのすべての経路を比較することで求めることができます。そして、点(X，Y)への経路数は、その点に合流する斜線があるかどうかによって下記のように異なります。
斜線がある場合
横方向の経路、縦方向の経路、斜め方向の経路の3種類
※図2の場合、点(2,2)、点(1,3)、点(3,1)等
斜線がない場合
横方向の経路、縦方向の経路の2種類
※図2の場合、点(4,2)、点(3,3)、点(3,2)、など
pm08_6.png
移動距離に関しては、問題文より以下のことがわかります。
  • 点(X，Y)から点(X＋1，Y)又は点(X，Y＋1)への移動距離は1となる。
    → 横方向と縦方向の移動距離は1と数える
  • 点(X，Y)から点(X＋1，Y＋1)への移動距離は0となる。
    → 斜め方向の移動距離は0と数える
よって、点(X，Y)の最短移動距離 D[X, Y] は以下のように求めることができます。
斜線がある場合
D[X-1, Y-1]、D[X-1, Y]+1、D[X, Y-1]+1 のうち最小の値
※プログラムのα部分
斜線がない場合
D[X-1, Y]+1、D[X, Y-1]+1 のうち最小の値
※プログラムのβ部分
エディットグラフでは str1[X] と str2[Y] が文字が一致したとき、点(X, Y)から点(X+1, Y+1)に向かって斜線が引かれます。よって、点(X, Y)が斜線の合流点であるか否かを判断するには、str1[X-1] と str2[Y-1] の一致を確認すれば良いことになります。プログラムのα部分の処理は斜線がある場合の処理ですから、2つの文字が一致するときに真となるように str1[X-1] == str2[Y-1] を条件式とするのが適切です。

「イ」は文字が一致しないときにα部分を実行することになるので誤り、「ウ」「エ」は各文字列の1文字目が全く無視されてしまうこと（ループ変数が1から始まる）及び上記の仕様上調べる位置が異なるので誤り、「オ」「カ」は同じ文字列の隣り合う文字を比較しているので誤りです。

∴a＝ア：str1[X-1] = str2[Y-1]

〔bについて〕
問題文より、点(0，0)から点(Str1Len，Str2Len)までの最短移動距離が編集距離となることがわかります。ループ処理では D[1, 1]から点ごとに最短移動距離を求め、最終的に D[Str1Len，Str2Len]（エディットグラフの右上の点に相当）への最短距離を求めています。よって、シンプルに D[Str1Len，Str2Len] の値を返すことになります。

∴b＝ウ：D[Str1Len，Str2Len]
広告

設問2

次の記述中の　に入れる正しい答えを，解答群の中から選べ。

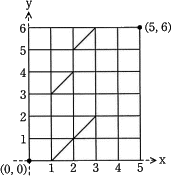
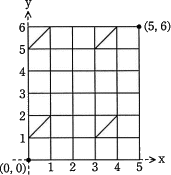
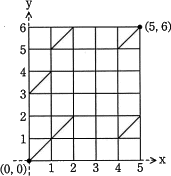
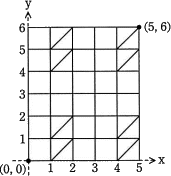
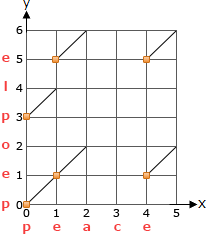
　Str1[]＝"peace"，Str2[]＝"people"の場合のエディットグラフはcとなる。
　CalcEditDistance("peace"，5，"people"，6)を実行した場合，関数 CalcEditDistance が終了するまでに行αはd回実行され，行βはe回実行される。また，返却値はfとなる。ここで，関数 CalcEditDistance 中のa，bには正しい答えが入っているものとする。
c に関する解答群
  • pm08_5a.png
  • pm08_5i.png
  • pm08_5u.png
  • pm08_5e.png
  • pm08_5o.png
d に関する解答群
  • 2
  • 4
  • 6
  • 8
  • 10
  • 12
  • 14
  • 16
e に関する解答群
  • 14
  • 16
  • 18
  • 20
  • 22
  • 24
  • 26
  • 28
f に関する解答群
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
解答選択欄
  • c:
  • d:
  • e:
  • f:
  • c=ウ
  • d=ウ
  • e=カ
  • f=イ

解説

〔cについて〕
文字列Str1"peace"の文字数は5、文字列Str2"people"の文字数は6です。図2の例を参考にすると、Str1がX軸側に配置され、Str2がY軸側に配置されるので、横5×縦6のエディットグラフになります。
pm08_7.png
2つの文字列の中で同一文字の組は以下の6つです。
  • Str1[0]とStr2[0]
  • Str1[0]とStr2[3]
  • Str1[1]とStr2[1]
  • Str1[1]とStr2[5]
  • Str1[4]とStr2[1]
  • Str1[4]とStr2[5]
各線に2つの文字列の文字を対応させたとき、同じ文字が交差する点から右上の点に線分を引くと次のようになります。
pm08_8.png
∴c＝ウ

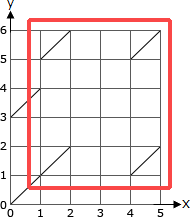
〔d、dについて〕
αおよびβが記述されているループ文は、Xを1からStr1Lenまで1ずつ増やしながら、Yを1からStr2Lenまで1ずつ増やしながら繰り返します。Str1Len=5、Str2Len=6なので、ループが繰り返される回数は「5×6＝30回」です。上記のエディットグラフ上の以下の範囲に含まれる点について処理を行うと考えてください。
pm08_9.png
このうちα部分は、Str1[X-1] と Str2[Y-1] が同一文字の場合に実行される部分なので実行される回数は6回（斜線の合流点に当たる点）、β部分はそれ以外のときの処理なので「30－6＝24回」となります。

∴d＝ウ：6
　e＝カ：24

〔fについて〕
縦移動および横移動は移動距離が1、斜め移動は移動距離が0なので、移動距離を短くするには斜め移動を可能なだけ多用する必要があります。

今回のエディットグラフの形状だと、点(0,0)→点(1,1)、点(1,1)→点(2,2)、点(4,5)→点(5,6) の3つの斜め移動を使い、それに縦横移動を組み合わせるのが最短移動距離となります。例えば以下のような経路です。
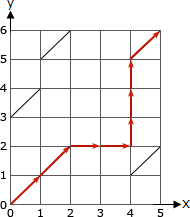
pm08_10.png
どの最短経路でも右上の点までたどり着くまでに、斜めの移動3回、縦横の移動が5回発生します。よって、最短移動距離は、

　0×3回＋1×5回＝5

以上より、Str1="peace"、Str2="people"の場合の関数 CalcEditDistance の返却値は「5」とわかります。

∴f＝イ：5
広告
広告

前の問題次の問題

▲
Pagetop