平成31年春期試験午後問題 問9

問9 ソフトウェア開発(C)
次のCプログラムの説明及びプログラムを読んで,設問1,2に答えよ。
入力ファイルを読み込んで,文字コードごとの出現回数を印字するプログラムである。
〔プログラムの説明〕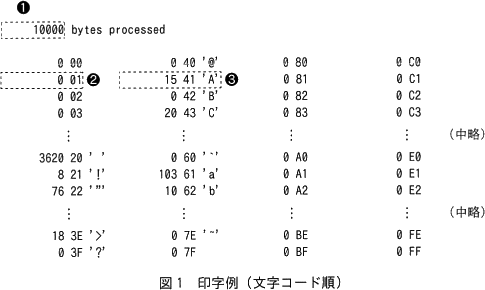

入力ファイルを読み込んで,文字コードごとの出現回数を印字するプログラムである。
〔プログラムの説明〕
- 入力ファイルは,バイナリファイルとして読み込む。入力ファイル中の各バイトの内容(ビット構成)に制約はない。入力ファイル名は,#defineで指定する。
- 入力ファイル中の各バイトについて,文字コード(16進数00~FFで表示する)ごとの出現回数を求めて印字する。印字例を,図1に示す。
- 印字様式を次に示す(記号❶,❷,❸は,図1中の記号を指している)。
- 1行目に,処理したバイト数を❶の形式で印字する。
- 3行目以降に,出現回数とその文字コードを❷の形式で印字する。ただし,文字コードが20~7Eの場合は,文字コードの後にそれが表す文字(文字は,この冊子の末尾にあるアセンブラ言語の仕様の1.3で規定するもの)を❸の形式で印字する。文字コードは,64行×4列の範囲に,上から下,左から右に文字コードの昇順となるように並べる。
- プログラム中で使用している関数 fgetc(s) は,ストリーム s から1文字を読み込んで返す。ストリームが入力ファイルの終わりに達しているときはEOFを返す。
- 入力ファイルのサイズは,long型(32ビットとする)で表現できる数値の範囲を超えないものとする。


広告
設問1
プログラム中の に入れる正しい答えを,解答群の中から選べ。
a に関する解答群
- cnt - 1
- cnt
- cnt + 1
b,c に関する解答群
- 4
- 64
- 256
- i + 4
- i + 64
- i + 192
解答選択欄
- a:
- b:
- c:
- a=イ
- b=カ
- c=イ
解説
〔aについて〕printf文が出力する文字列の一部に"bytes processed"があること、プログラム中で最初の出力であることから印字例の❶の出力処理であるとわかります。aはフォーマット指定子"%10ld"の部分に入る値ですので、「処理したバイト数」を表す変数が入ります。
選択肢として与えられた変数 cnt は、while文内の「cnt++」が実行された回数だけ増加します。このwhile文の条件としては「(chr = fgetc(infile)) != EOF」が与えられています。これはC言語では定番の処理で、ファイルの内容を先頭から1文字ずつ読み込むことをファイルの終端(EOF)に達するまで行うときに使われます。
変数 cnt はEOFでない文字を読み込んだときにインクリメント(+1)されるため、cnt の数がそのまま処理した文字数になります。
∴a=イ:cnt
〔bcについて〕
便宜上、プログラム中の2つのfor文を以下のように呼びます。
for (i=0; i<64; i++) ・・・for文1
for (chr=i; chr<[b]; chr+=[c]) ・・・for文2
まず、for文1の最後の処理で改行「printf("\n")」を実施していることから、for文1の1ループで1行の出力を行うこと、for文2で1行に4列を出力する処理を行っていることがわかります。つまりfor文2の繰返し回数は常に4回となるべきです。for (chr=i; chr<[b]; chr+=[c]) ・・・for文2
プログラムでは256種類の文字コードの出現回数が freq[0]~freq[255] に格納されており、図1中の配列 freq のみに注目した場合、以下のような添字で配列 freq を出力する必要があります。

出力を見ると、chrが0のときは192を超えたら終了、chrが1のときは193を超えたら終了、…、chrが63のときは255を超えたら終了というように、for文2は i の値に「64×3=192」を加えた値以下の間だけ繰り返せばよいことがわかります。よって、bには「i+192」が入ります。
∴b=カ:i+192
各列の freq の添字は64ずつ離れているので、for文2では、0→64→128→192 というように chr を64ずつ増やしながら4回実行することになります。よって、cには「64」が入ります。
∴c=イ:64
広告
設問2
次の記述中の に入れる正しい答えを,解答群の中から選べ。ここで,記述中のbとcには,設問1の正しい答えが入っているものとする。
文字コードを出現回数の降順に並べて印字する処理を追加する。追加した処理による印字例を,図2に示す。印字の様式は,文字コードの並び順を除いて,図1の3行目以降の様式と同じである。同じ出現回数の文字コードは,それらを文字コードの昇順に並べる。 この処理のために,プログラムの行①の直後に,次の宣言を追加する。
この処理のために,プログラムの行①の直後に,次の宣言を追加する。
int ih,ix,code[256]
さらに,プログラムの行②の位置に,次の整列処理部を追加する。 ここで,整列処理部で使用する Swap(x,y) は,xとyの内容を入れ替えるために用意したマクロである。
ここで,整列処理部で使用する Swap(x,y) は,xとyの内容を入れ替えるために用意したマクロである。
整列処理部では,整列対象のデータ数が比較的少なく,また同じ出現回数の文字コードは元の並び順が維持されるので,バブルソートを使用している。
行④のwhile文のブロックを1回実行すると,配列の走査範囲(要素番号0~ih)中の出現回数の最小値とその文字コードが,要素番号 ih の位置に置かれ,配列の走査範囲が1だけ狭められる。これを繰り返して整列を行う。この処理ではwhile文のブロックの実行回数は常にd回となる。
ここで,while文のブロックの1回の繰返しにおいて,行⑥のif文のブロック内の処理が最後に実行されたときの i の値を ix とすると,行⑤のfor文のブロックの実行が終了した時点で,配列 freq の要素番号e以降の要素の値は整列済みとなっている。これを利用して,整列処理部を表1に示すように変更すれば,while文のブロックの実行回数を減らせる可能性がある。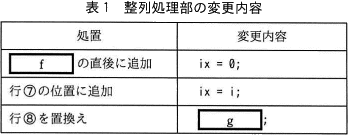
文字コードを出現回数の降順に並べて印字する処理を追加する。追加した処理による印字例を,図2に示す。印字の様式は,文字コードの並び順を除いて,図1の3行目以降の様式と同じである。同じ出現回数の文字コードは,それらを文字コードの昇順に並べる。

int ih,ix,code[256]
さらに,プログラムの行②の位置に,次の整列処理部を追加する。

整列処理部では,整列対象のデータ数が比較的少なく,また同じ出現回数の文字コードは元の並び順が維持されるので,バブルソートを使用している。
行④のwhile文のブロックを1回実行すると,配列の走査範囲(要素番号0~ih)中の出現回数の最小値とその文字コードが,要素番号 ih の位置に置かれ,配列の走査範囲が1だけ狭められる。これを繰り返して整列を行う。この処理ではwhile文のブロックの実行回数は常にd回となる。
ここで,while文のブロックの1回の繰返しにおいて,行⑥のif文のブロック内の処理が最後に実行されたときの i の値を ix とすると,行⑤のfor文のブロックの実行が終了した時点で,配列 freq の要素番号e以降の要素の値は整列済みとなっている。これを利用して,整列処理部を表1に示すように変更すれば,while文のブロックの実行回数を減らせる可能性がある。

d に関する解答群
- 253
- 254
- 255
- 256
e に関する解答群
- 256 - ix
- ix - 1
- ix
- ix + 1
f に関する解答群
- 行③
- 行④
- 行⑤
g に関する解答群
- ih = ix - 1
- ih = ix
- ih = ix + 1
- ix = ih
解答選択欄
- d:
- e:
- f:
- g:
- d=ウ
- e=エ
- f=イ
- g=イ
解説
〔整列処理部について〕整数処理部のプログラムは、バブルソートにより配列を出現回数の降順に成立する処理と、それを印字する処理で構成されています。設問ではバブルソートのみについて問うているので、印字部分の解説は割愛します。
最初にバブルソートについて説明します。
バブルソート(基本交換法)とは、全ての要素について隣接する要素と比較し、順序が逆であれば入れ替える操作を、(要素数-1)回繰り返すことで整列を行うアルゴリズムです。
〔整数処理部〕の for(i=0; i<ih; i++)の部分では、配列 freq のih 番目までの要素比較を実施しています。配列 freq のi番目とi+1番目を比較し、i番目のほうが出現回数が低い場合、要素iと要素i+1の入れ替えが発生します。この処理を繰り返すとfor文が終了した段階で、配列freqのih番目には、0~ih番目の中で一番出現回数の小さい要素が格納されています。
最初に ih は255で初期化されています。ih=255でfor文を実行すると、配列 freq の0~255番目の中で一番低い数が freq[255] に格納されます。
次に、ih--が実行され、ihは254になります。同様にfor文を実行すると、配列 freq の0~254番目の中で一番低い数が freq[254] に格納されます。
この処理を ih が 0になるまで繰り返して配列 freq の降順ソートを実施します。
〔dについて〕
変数 ih は255で初期化され、while文の最後にデクリメント(-1)されます。また、while文は ih が0より大きい間実行され、途中break文でブロックを抜けることもありません。つまり、whileブロックは ih が 255~1の間繰り返されます。よって、whileブロックの実行回数は常に「255回」となります。
∴d=ウ:255
〔eについて〕
本文中の「ここで,while文のブロックの1回の繰返し…」の段落では、バブルソートを良くするための改良案が記載されています。少しわかりにくい部分があるので例を交えながら解説します。
仮に以下のような配列Xのバブルソート(降順)を考えます。
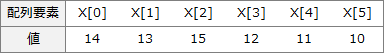
for文1回を実行すると、配列Xの0番目から5番目の中で最も小さい値がX[5]に格納されます。既にX[3]以降は降順に整列済なので、このとき入れ替えが発生するのは X[1]とX[2]の入れ替えだけです。
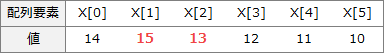
配列Xの例より、i=1を最後に要素の入れ替えが発生しなかった場合、X[2]以降は既にソート済みと考えることができます。設問中にあるように、入れ替えが最後に行われたときの i の値を ix とすると、X[ix+1]以降はすでにソート済みと考えることができます。よって、eには「ix+1」が入ります。
∴e=エ:ix+1
〔fについて〕
ixを初期化する処理をプログラム中のどこに入れるかが問われています。
0番目からih番目までの中で、最後に要素が入れ替わった番号を知りたいため、for文の直前(while文の直後)に初期化する必要があります。よって④が正解です。
③の位置に入れた場合、ih=0となる前に完全ソート済となった際に、以降のfor文でixの値が更新されず、ihが同じ値のままなので永久にwhileブロックから抜けることができなくなってしまいます。また、⑤の位置に入れた場合、入れ替えが発生した際にixにiを代入しても、次のfor文で0に初期化されてしまいます。
∴f=イ:④
〔gについて〕
ih を更新する値が問われています。
配列Xを使用した例では、ih=5のとき、i=1で最後の要素入れ替えが発生しました。このときX[2]以降がソート済みとなり、次のwhileブロックではX[1]までの要素を比較するだけで済みます(ihが1未満の間for文を実行する)。同様に、i=ixで最後の要素入れ替えが発生した場合、次のwhileブロックではX[ix]までの要素を比較する必要があります。よって、次回の整列対象範囲を決める ih に ix の値を代入すれば期待通りに動作します。
∴g=イ:ih=ix
広告
広告