平成31年春期試験午後問題 問11

問11 ソフトウェア開発(Java)
次のJavaプログラムの説明及びプログラムを読んで,設問1,2に答えよ。
(Javaプログラムで使用するAPIの説明は,こちらを参照してください。)
〔プログラムの説明〕
升(ます)目を用いて表現された迷路と,迷路上に置かれて外部から操作される駒を表すプログラムである。
迷路は,駒が通れる升(以下,通路という)と通れない升(以下,壁という)から成る。迷路の外周は壁である。通路のうちの一つが開始地点であり,開始地点でない通路のうちの一つがゴール地点である。本問で扱う迷路を,図1に示す。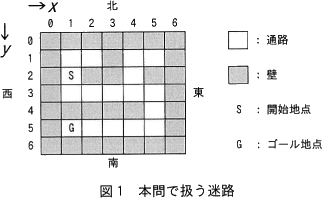 迷路上の升の位置は,2次元の座標(x,y)で表す。xとyはともに非負整数である。ある位置を基準として,xの値が大きくなる方角を東,小さくなる方角を西,yの値が大きくなる方角を南,小さくなる方角を北とする。
迷路上の升の位置は,2次元の座標(x,y)で表す。xとyはともに非負整数である。ある位置を基準として,xの値が大きくなる方角を東,小さくなる方角を西,yの値が大きくなる方角を南,小さくなる方角を北とする。
駒は,東西南北のいずれかを向いており,向いている方角を基準として,次の三つの操作を外部から受け付ける。
(Javaプログラムで使用するAPIの説明は,こちらを参照してください。)
〔プログラムの説明〕
升(ます)目を用いて表現された迷路と,迷路上に置かれて外部から操作される駒を表すプログラムである。
迷路は,駒が通れる升(以下,通路という)と通れない升(以下,壁という)から成る。迷路の外周は壁である。通路のうちの一つが開始地点であり,開始地点でない通路のうちの一つがゴール地点である。本問で扱う迷路を,図1に示す。

駒は,東西南北のいずれかを向いており,向いている方角を基準として,次の三つの操作を外部から受け付ける。
- 左の方向に向きを変える。
- 右の方向に向きを変える。
- 隣接する前方の升が通路なら,1升前進する。
- クラス Maze は迷路を表す。コンストラクタの引数には,文字列で表現した迷路と,迷路の西端から東端までの升の個数を指定する。迷路を表現する文字列は,1升を表す文字を西から東に向かって順に並べた1行分の文字列を,北から南に向かって順に連結したものである。升の種類は,char型の値で表す。"*"は壁を,それ以外の値は通路を表し,"S"は開始地点を,"G"はゴール地点を表す。引数に誤りはないものとする。
メソッド getStartLocation は開始地点の座標を返す。メソッド isGoal は指定された座標の升がゴール地点であればtrueを,それ以外はfalseを返す。メソッド isBlank は指定された座標の升が通路ならばtrueを,壁ならばfalseを返す。 - クラス Piece は,迷路上に置かれる駒を表す。コンストラクタの引数で迷路を指定する。インスタンスは,最初は,開始地点に位置し,北を向いている。
メソッド turnLeft は左の方向に,turnRight は右の方向に向きを変える。
メソッド tryStepForward は,隣接する前方の升が通路なら1升前進し,前進した方角を履歴リストに追加してからtrueを返す。通路でなければ,前進せずにfalseを返す。
メソッド isAtGoal は,ゴール地点にいればtrueを,それ以外はfalseを返す。
メソッド getHistory は,履歴リストを返す。 - 列挙 Direction は,方角を表す。
メソッド left は列挙定数が表す方角に向かって左の方角を,right は右の方角を返す。 - クラス Location は,迷路上の升の位置を示す座標を表す。
- クラス PlayMaze は,図1に示す開始地点からゴール地点に至るまで駒を操作し,その後,履歴リストを表示する。

広告
設問1
プログラム中の に入れる正しい答えを,解答群の中から選べ。
a,b に関する解答群
- %
- &
- *
- +
- -
- /
- ^
- |
c に関する解答群
- direction
- direction.dx,direction.dy
- location + direction
- location.x + direction.dx,location.y + direction.dy
d に関する解答群
- (ordinal() + 3) % 4
- (ordinal() + 3) / 4
- (ordinal() - 1) % 4
- (ordinal() - 1) / 4
解答選択欄
- a:
- b:
- c:
- d:
- a=ウ
- b=ア
- c=エ
- d=ア
解説
〔bについて〕まず[b]について解説をしていきます。
[b]は Maze クラスの locationOf メソッドの中の処理にあります。locationOf メソッドはどこで呼び出されているかというと、Maze クラスの Maze メソッドの中で startLocation に格納するための値を取得するために利用されています。
locationOf メソッドでは、まずint型の index に mazeData の indexOf(c)(cの位置を返す関数)の結果を格納しています。では、Maze クラスの mazeData には何が格納されるのかを追ってみましょう。
mazeData に値を格納している箇所を探してみると、Maze メソッドの中で値の格納が行われています。Maze メソッドは、PlayMaze クラスの main の中で迷路の構造と横の長さ、二つを引数として Maze インスタンスを定義したときに呼び出されす。つまり、mazeData にはString型で定義された迷路の構造そのものが入るのです。mazeData にはString型の迷路の構造が入りますが、データ上は下記のように1行の文字列のようになっています(*が壁)。
"********..*..**S**.*** … ..******.**G … ..********"
ここで locationOf メソッドに戻ってみましょう。問題文には「メソッド getStartLocation は開始地点の座標を返す」と書いており、getStartLocation では startLocation を return しています。このことから startLocation は、迷路の開始位置の座標を保持するメンバー変数(finalが付いているので定数)であることがわかると思います。locationOf の返り値は Location クラスなので、locationOf メソッドは、1行のデータを2次元として見たときのスタート地点(S)のx座標、y座標を返さなければなりません。
Maze インスタンスが呼び出されたときに迷路の横の長さを表す width が定義されることになりますが、この width を使ってString型の迷路の構造を表す mazeData を加工する必要があります。5×7の迷路を例にすると、mazeData 上の文字順と迷路状の位置の対応は以下のようになります。
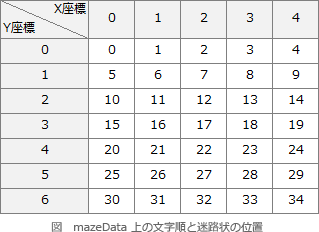
- 26 → x座標:26 % 5 = 1、y座標:26 / 5 = 5
- 3 → x座標:3 % 5 = 3、y座標:3 / 5 = 0
∴b=ア:%
〔aについて〕
まずは[a]の処理がある isGoal メソッドがどこで呼ばれているかを把握しましょう。Maze クラスの isGoal メソッドは Piece クラスの isAtGoal メソッドで呼び出されています。isAtGoal メソッドでは Piece クラスが持つprivate変数である location を引数として渡しています。
location には Location クラスのインスタンスが格納されていますが、どんな内容が入るのか確認してみましょう。Location クラスでは x と y の変数が用意されており、問題文とその名称から、xとyの座標を表していることがわかると思います。
Piece クラスの中の変数の location は、同クラスの Piece メソッドが呼ばれた際にまず maze.getStartLocation() を実行した返り値が入り、tryStepForward メソッドによって順次更新されることが読み取れます。順次更新された location に対し、main の中でループで isAtGoal メソッドを呼び出してゴールにたどり着いたかどうかを判断しています。すなわち isAtGoal メソッドでは、location に格納されたx座標、y座標とString型の迷路の構造が入った mazeData を材料としてゴールにたどり着いたかどうかを判断する処理が入ります。
location のx座標、Y座標から対応する mazeData の文字位置を得るには、先程とは逆にy座標に width で掛けたものにx座標を加えることになります。仮に width=5 ならば、
- (x=2,y=2) → 5×2+2=12
- (x=0,y=5) → 5×5+0=25
∴a=ウ:*
〔cについて〕
Locationインスタンスを作成する上でどんな引数を渡すかについて問われています。
最初に Location クラスの Location メソッドを確認してみましょう。
一つ目の引数を x に、二つ目の引数を y に代入しているため、[c]では一つ目の引数にx座標、二つ目の引数にy座標を渡していると判断できます。[c]が含まれる tryStepForward メソッドについて、問題文には「隣接する前方の升が通路なら1升前進し,前進した方角を履歴リストに追加してからtrueを返す。通路でなければ,前進せずにfalseを返す」と書かれており、main メソッドのループの中で piece.isAtGoal() がtrueになるまで tryStepForward メソッドが呼び出されることがわかります。
tryStepForward メソッドの役割と、[c]の処理の下に「指定された座標の升が通路ならばtrueを,壁ならばfalseを返す」処理をする isBlank メソッドがあることから、[c]が問われている行では、駒が現在向いている方角に1マス分移動した場合の位置(x座標、y座標)を nextlocation に入れていることがわかると思います。
direction は列挙型で、以下の定数が定義されています。
NORTH(0, -1), EAST(1, 0), SOUTH(0, 1), WEST(-1, 0)
各列挙型定数の値は、駒がその方角に進んだときに現在の座標値に加減する値を保持しています。ここまでを踏まえて選択肢を見ると、今の位置を更新しているようには見えない「ア」と「イ」の選択肢は除外されます。さらに、location インスタンスと direction インスタンスの足し算をしていて文法的におかしい「ウ」も選択肢から省かれます。
よって、[c]にはx座標、y座標それぞれに対して、location インスタンスに格納されている座標に direction インスタンスに格納されている座標を足し合わせている「エ」が正解となります。
∴c=エ:location.x + direction.dx,location.y + direction.dy
〔dについて〕
[d]はenum型(列挙型)の Direction の中の left メソッドの中にあり、問題文では left メソッドは左の方角を向くための関数であると記載されています。
left メソッドの処理を考える上で、既に問題文に記載されている right メソッドの処理が非常に参考になります。現在向いている方角に対して right メソッドが実行されると列挙型の定義順がどのように変わっていくか具体的に考えてみます。right メソッドは現在の方角の右の方角を返すので、以下のように遷移します。
- NOATH(enum型の0番目) → EAST(enum型の1番目)
- EAST(enum型の1番目) → SOUTH(enum型の2番目)
- SOUTH(enum型の2番目) → WEST(enum型の3番目)
- WEST(enum型の3番目) → NOATH(enum型の0番目)
次に left メソッドによって列挙型の定義順がどうなっていくかを考えます。left メソッドは現在の方角の左の方角を返すので、以下のように遷移します。
- NOATH(enum型の0番目) → WEST(enum型の3番目)
- WEST(enum型の3番目) → SOUTH(enum型の2番目)
- SOUTH(enum型の2番目) → EAST(enum型の1番目)
- EAST(enum型の1番目) → NOATH(enum型の0番目)
- NOATH(enum型の0番目) → WEST(enum型の3番目)
∴d=ア:(ordinal() + 3) % 4
広告
設問2
プログラム5のαの位置に次の処理を挿入し,実行結果として,図2に示す方角のリストを得た。駒は,開始地点からリストの方角の順に1升ずつ進むと,直前の升に戻る(正反対の方角に向きを変えて進む)ことなく,ゴール地点に至ることができる。 に入れる正しい答えを,解答群の中から選べ。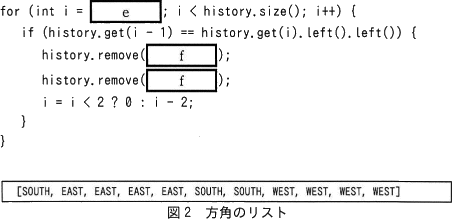

e に関する解答群
- -1
- 0
- 1
f に関する解答群
- i
- i + 1
- i - 1
解答選択欄
- e:
- f:
- e=ウ
- f=ウ
解説
〔eについて〕[e]はプログラムの意味を考えることなく解くことができます。
for文内部の1行目にある history.get(i - 1) に注目してみてください。[e]ではforループの初期値を定義することになりますが、「ア」の-1、「イ」の0だと get の引数が負数となりエラーが発生してしまいます。よって、エラーにならない「1」が正解となります。
∴e=ウ:1
〔fについて〕
remove は要素の削除を表すメソッドです。[f]は引数としてListのインデックスが入り、history.remove(f) でどのインデックスの要素を削除対象とすべきかを問われています。
このforループでは、history の0番目と1番目、1番目と2番目、…というように隣り合った要素を比較しながら処理していきますが、2要素の削除が行われるのは次の条件式の結果が真となる場合です。
if (history.get(i - 1) == history.get(i).left().left())
history の要素には方角を表すenum型の direction が入り、left メソッドは左の方角を返す関数であることから、上記のif文ではあるインデックスの位置の要素に対して、次のインデックスの位置の要素が正反対の方角であるかどうかを確認する条件分岐であることがわかります。仮に i に3が入るとして、
- history.get(2)の値がNOATH
- history.get(3)の値がSOUTH
設問2の問題文の「リストの方角の順に1升ずつ進むと,直前の升に戻る(正反対の方角に向きを変えて進む)ことなく,ゴール地点に至る」という表現があります。北に進んで南に進む等は直前の升に戻るだけで無駄ですから取り除いてしまおうというわけです。上記の例では history の2番目の要素と history の3番目の要素の2つを削除することが必要となってきます。i=3として場合の各選択肢の動作は次の通りです(List型の最初の要素を0番目とします)。
- historyの3番目の要素を削除
↓
historyの4番目の要素が、3番目に移動する
↓
historyの3番目の要素を削除
結果としてhistoryの3、4番目を削除することになるので不適切です。 - historyの4番目の要素を削除
↓
historyの5番目の要素が、4番目に移動する
↓
historyの4番目の要素を削除
結果としてhistoryの4、5番目を削除することになるので不適切です。 - historyの2番目の要素を削除
↓
historyの3番目の要素が、2番目に移動する
↓
historyの3番目の要素を削除
結果としてhistoryの2、3番目を削除することになるので適切な処理です。
広告
広告