サンプル問題 [科目B]問4

問4解説へ
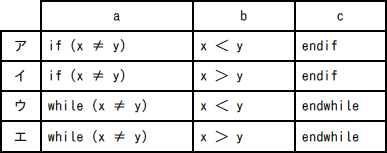
次のプログラム中のa~cに入れる正しい答えの組合せを,解答群の中から選べ。
関数 gcd は,引数で与えられた二つの正の整数 num1 と num2 の最大公約数を,次の(1)~(3)の性質を利用して求める。
関数 gcd は,引数で与えられた二つの正の整数 num1 と num2 の最大公約数を,次の(1)~(3)の性質を利用して求める。
- num1 と num2 が等しいとき,num1 と num2 の最大公約数は num1 である。
- num1 が num2 より大きいとき,num1 と num2 の最大公約数は,(num1 - num2) と num2 の最大公約数と等しい。
- num2 が num1 より大きいとき,num1 と num2 の最大公約数は,(num2 - num1) と num1 の最大公約数と等しい。

正解 エ問題へ
分野:アルゴリズムとプログラミング
カテゴリ:プログラムの基本要素
カテゴリ:プログラムの基本要素
広告
解説
まず、aとcに入る制御文ですが、(1)の説明に最大公約数は num1 と num2 が等しくなったときの num1 の値であるという説明があります。2つの正の整数について、(2)または(3)の処理を1回行っただけでは num1 と num2 が等しくなるとは限らず、両者が等しくなるまで(2)または(3)の処理を繰り返す必要があるので、繰返し処理を行うwhile文が当てはまります。よって、正解肢は「ウ」または「エ」に絞られます。
bでは、条件に合致するときにx ← x - y、つまり、num1 に num1 - num2 を代入する処理を行っています。(2)の説明より、この処理を行うのは num1 が num2 より大きいときですから、x > yが当てはまるとわかります。
逆にx < yのときにこの処理を行ってしまうと、x の値は負数となり、それ以後x < y⇒x ← x - yが永遠に繰り返されることにより、繰返し処理が終了しなくなってしまいます。また、2つの正の整数の最大公約数が負数ということはありません。よって、x < yを入れるのは不適切です。
したがって、while文とx > yの組合せである「エ」が適切です。
【参考】
このアルゴリズムは、最大公約数を求める有名な手法である「ユークリッドの互除法」の実装です。
例えば、num1 = 36、num2 = 60 とすると、
bでは、条件に合致するときにx ← x - y、つまり、num1 に num1 - num2 を代入する処理を行っています。(2)の説明より、この処理を行うのは num1 が num2 より大きいときですから、x > yが当てはまるとわかります。
逆にx < yのときにこの処理を行ってしまうと、x の値は負数となり、それ以後x < y⇒x ← x - yが永遠に繰り返されることにより、繰返し処理が終了しなくなってしまいます。また、2つの正の整数の最大公約数が負数ということはありません。よって、x < yを入れるのは不適切です。
したがって、while文とx > yの組合せである「エ」が適切です。
【参考】
このアルゴリズムは、最大公約数を求める有名な手法である「ユークリッドの互除法」の実装です。
例えば、num1 = 36、num2 = 60 とすると、
num1 < num2 なので、num2 ← 60 - 36 = 24
⇒num1 = 36、num2 = 24
num1 > num2 なので、num1 ← 36 - 24 = 12
⇒num1 = 12、num2 = 24
num1 < num2 なので、num2 ← 24 - 12 = 12
⇒num1 = 12、num2 = 12
num1 = num2 なので、最大公約数は12
という手順で2つの自然数の最大公約数を求めます。⇒num1 = 36、num2 = 24
num1 > num2 なので、num1 ← 36 - 24 = 12
⇒num1 = 12、num2 = 24
num1 < num2 なので、num2 ← 24 - 12 = 12
⇒num1 = 12、num2 = 12
num1 = num2 なので、最大公約数は12
広告