2022年4月25日公開分 [科目B]問4

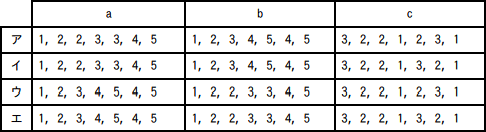
　次の記述中のa～cに入れる正しい答えの組合せを，解答群の中から選べ。ここで，配列の要素番号は1から始まる。

　要素の多くが0の行列を疎行列という。次のプログラムは，二次元配列に格納された行列のデータ量を削減するために，疎行列の格納に適したデータ構造に変換する。関数 transformSparseMatrix は，引数 matrix で二次元配列として与えられた行列を，整数型配列の配列に変換して返す。関数 transformSparseMatrix を transformSparseMatrix({{3，0，0，0，0}，{0，2，2，0，0}，{0，0，0，1，3}，{0，0，0，2，0}，{0，0，0，0，1}})として呼び出したときの戻り値は，{{a}，{b}，{c}} である。

〔プログラム〕

正解　イ問題へ

分野：アルゴリズムとプログラミング
カテゴリ：プログラミングの諸分野への適用

解説

引数 matrix は以下の5つの配列を要素として保持する二次元配列です。

matrix = {
　1: {3, 0, 0, 0, 0},
　2: {0, 2, 2, 0, 0},
　3: {0, 0, 0, 1, 3},
　4: {0, 0, 0, 2, 0},
　5: {0, 0, 0, 0, 1}
}

この配列を引数としてプログラムを呼び出すと、以下のように処理されていきます。

sparseMatrix ← {{}, {}, {}}
matrix[1] = {3, 0, 0, 0, 0}の要素ひとつずつ（matrix[1, j]）を見て、値が0でなければ以下を行う。
- sparseMatrix[1]の末尾にiの値を追加する
- sparseMatrix[2]の末尾にjの値を追加する
- sparseMatrix[3]の末尾にmatrix[i, j]の値を追加する
matrix[1]のうち0でないのは1番目の要素"3"だけなので、i、j、matrix[1, j]の値をそれぞれ配列 sparseMatrix に追加する。
sparseMatrix[1] に i=1 を追加 ⇒ {1}
sparseMatrix[2] に j=1 を追加 ⇒ {1}
sparseMatrix[3] に matrix[1, 1]=3 を追加 ⇒ {3}
matrix[2] = {0, 2, 2, 0, 0}の要素ひとつずつ（matrix[2, j]）を見て、2.と同じ処理を行う。matrix[2]のうち0でないのは2番目の要素"2"および3番目の要素"2"だけなので、i、j、matrix[2, j]の値をそれぞれ配列 sparseMatrix に追加する。
//j = 2 のときの処理
sparseMatrix[1] に i=2 を追加 ⇒ {1, 2}
sparseMatrix[2] に j=2 を追加 ⇒ {1, 2}
sparseMatrix[3] に matrix[2, 2]=2 を追加 ⇒ {3, 2}
//j = 3 のときの処理
sparseMatrix[1] に i=2 を追加 ⇒ {1, 2, 2}
sparseMatrix[2] に j=3 を追加 ⇒ {1, 2, 3}
sparseMatrix[3] にmatrix[2, 3]=2 を追加 ⇒ {3, 2, 2}
ここまでの処理で、空欄aの先頭が{1, 2, 3, …}となっている「ウ」「エ」は誤りだとわかります。
matrix[3] = {0, 0, 0, 1, 3}の要素ひとつずつ（matrix[3, j]）を見て、2.と同じ処理を行う。matrix[3]のうち0でないのは4番目の要素"1"および5番目の要素"3"だけなので、i、j、matrix[3, j]の値をそれぞれ配列 sparseMatrix に追加する。
//j = 4 のときの処理
sparseMatrix[1] に i=3 を追加 ⇒ {1, 2, 2, 3}
sparseMatrix[2] に j=4 を追加 ⇒ {1, 2, 3, 4}
sparseMatrix[3] に matrix[3, 4]=1 を追加 ⇒ {3, 2, 2, 1}
//j = 5 のときの処理
sparseMatrix[1] に i=3 を追加 ⇒ {1, 2, 2, 3, 3}
sparseMatrix[2] に j=5 を追加 ⇒ {1, 2, 3, 4, 5}
sparseMatrix[3] に matrix[3, 5]=3 を追加 ⇒ {3, 2, 2, 1, 3}
ここまでの処理で、空欄cの先頭が{{3, 2, 2, 1, 2, …}となっている「ア」は誤りであるとわかります。よって、消去法により正解は「イ」と判断できます。一応、この後の処理を最後までみていきましょう。
matrix[4] = {0, 0, 0, 2, 0}の要素ひとつずつ（matrix[4, j]）を見て、2.と同じ処理を行う。matrix[4]のうち0でないのは4番目の要素"2"だけなので、i、j、matrix[4, j]の値をそれぞれ配列 sparseMatrix に追加する。
sparseMatrix[1] に i=4 を追加 ⇒ {1, 2, 2, 3, 3, 4}
sparseMatrix[2] に j=4 を追加 ⇒ {1, 2, 3, 4, 5, 4}
sparseMatrix[3] に matrix[4, 4]=2 を追加 ⇒ {3, 2, 2, 1, 3, 2}
matrix[5] = {0, 0, 0, 0, 1}の要素ひとつずつ（matrix[5, j]）を見て、2.と同じ処理を行う。matrix[5]のうち0でないのは5番目の要素"1"だけなので、i、j、matrix[5, j]の値をそれぞれ配列 sparseMatrix に追加する。
sparseMatrix[1] に i=5 を追加 ⇒ {1, 2, 2, 3, 3, 4, 5}
sparseMatrix[2] に j=5 を追加 ⇒ {1, 2, 3, 4, 5, 4, 5}
sparseMatrix[3] に matrix[5, 5]=1 を追加 ⇒ {3, 2, 2, 1, 3, 2, 1}

したがって正しい組合せは「イ」です。

2022年4月25日公開分 [科目B]問4

前の問題次の問題