応用数学(全50問中10問目)

広告
解説
まず、式中の lim について簡単な例を交えて少し説明しておきます。
式中のある変数が限りなく0に近づいたときや、無限大(またはマイナスの無限大)に限りなく近づいたときの式の値を考えることを数列の極限といいます。極限値は lim の記号を用いて次の例のように表します。
これを踏まえて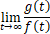 の値を求めます。
の値を求めます。
まず、g(t)ƒ(t) を変換すると次のような形になります。
g(t)ƒ(t)=bt2-t÷at+1=b(t+1)a(t2-t)
式中のtが増えると、b(10+1)a(102-10) → b(100+1)a(1002-100) → b(10000+1)a(100002-10000) → …というように分子の増加量よりも分母の増加量が多く0に近づいていくので、t→∞ のとき g(t)ƒ(t) の値は限りなく0に近づきます。
∴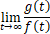 =0
=0
したがって「ア」が正解です。
式中のある変数が限りなく0に近づいたときや、無限大(またはマイナスの無限大)に限りなく近づいたときの式の値を考えることを数列の極限といいます。極限値は lim の記号を用いて次の例のように表します。
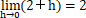 … hが限りなく0に近づいたとき 2+h の極限値は2である。
… hが限りなく0に近づいたとき 2+h の極限値は2である。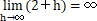 … hが限りなく無限大(∞)に近づいたとき 2+h の極限値は∞である。
… hが限りなく無限大(∞)に近づいたとき 2+h の極限値は∞である。
これを踏まえて
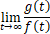 の値を求めます。
の値を求めます。まず、g(t)ƒ(t) を変換すると次のような形になります。
g(t)ƒ(t)=bt2-t÷at+1=b(t+1)a(t2-t)
式中のtが増えると、b(10+1)a(102-10) → b(100+1)a(1002-100) → b(10000+1)a(100002-10000) → …というように分子の増加量よりも分母の増加量が多く0に近づいていくので、t→∞ のとき g(t)ƒ(t) の値は限りなく0に近づきます。
∴
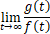 =0
=0したがって「ア」が正解です。
広告