分野：テクノロジ系
中分類：基礎理論
小分類：応用数学

相対誤差とは、真正な値に対する誤差の割合です。相対誤差を求めるには誤差を真正な値で割ります。

単純化した例として(ア)真正な値が5で近似値が6の場合と、(イ)真正な値が50で近似値が51の場合を考えてみます。
どちらの場合でも誤差は1ですが、相対誤差は、
　(ア)　1÷5＝0.2
　(イ)　1÷50＝0.02
となり、近似値の相対誤差は(ア)が(イ)の10倍にもなります。

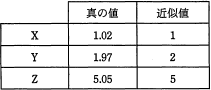
同様に三つの実数X～Zとそれぞれの近似値について相対誤差を求めると、
　X:　0.02÷1.02≒0.019
　Y:　0.03÷1.97≒0.015
　Z:　0.05÷5.05≒0.010

したがって相対誤差の小さい順に並べると「Z，Y，X」になります。