離散数学(全109問中66問目)

No.66解説へ
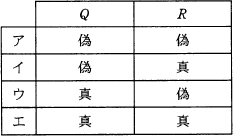
P,Q,Rはいずれも命題である。命題Pの真理値は真であり,命題(not P) or Q 及び命題(not Q) or R のいずれの真理値も真であることが分かっている。Q,Rの真理値はどれか。ここで,X or Y は X と Y の論理和,not X はXの否定を表す。
出典:平成19年秋期 問 9
広告
解説
命題Pが真とわかってるので、まずPが含まれている「(not P) or Q=真」について考えます。
Pが真なので「not P=偽」になります。したがってこの命題は「偽 or Q=真」と書き換えることができます。論理和演算(or演算)の特徴を考えると「偽 or Q=真」を満たすためにはQが真でなければならないので、命題Qは真ということがわかります。
次に「(not Q) or R=真」について考えます。Qが真なので「not Q=偽」、この命題は「偽 or R=真」と書き換えることができます。先程と同様に論理和演算の特徴から、この命題を満たすための命題Rは真であることがわかります。
これらをまとめるとQ,Rはいずれも真ということがわかるので、正解は「エ」になります。
Pが真なので「not P=偽」になります。したがってこの命題は「偽 or Q=真」と書き換えることができます。論理和演算(or演算)の特徴を考えると「偽 or Q=真」を満たすためにはQが真でなければならないので、命題Qは真ということがわかります。
次に「(not Q) or R=真」について考えます。Qが真なので「not Q=偽」、この命題は「偽 or R=真」と書き換えることができます。先程と同様に論理和演算の特徴から、この命題を満たすための命題Rは真であることがわかります。
これらをまとめるとQ,Rはいずれも真ということがわかるので、正解は「エ」になります。
広告