令和元年秋期試験午後問題　問8

午前試験免除制度対応！基本情報技術者試験のeラーニング【独習ゼミ】

問8　データ構造及びアルゴリズム

次のプログラムの説明及びプログラムを読んで，設問1～3に答えよ。

〔プログラムの説明〕
　関数 BitapMatch は，Bitap法を使って文字列検索を行うプログラムである。
　Bitap法は，検索対象の文字列(以下，対象文字列という)と検索文字列の照合に，個別の文字ごとに定義されるビット列を用いるという特徴をもつ。
　なお，本問では，例えば2進数の16ビット論理型の定数 0000000000010101 は，上位の0を省略して"10101"Bと表記する。
  • 関数 BitapMatch は，対象文字列を Text[] に，検索文字列を Pat[] に格納して呼び出す。配列の要素番号は1から始まり，Text[] のi番目の文字は Text[i] と表記する。Pat[] についても同様にi番目の文字は Pat[i] と表記する。対象文字列と検索文字列は，英大文字で構成され，いずれも最長16文字とする。
    対象文字列 Text[] が"AACBBAACABABAB"，検索文字列 Pat[] が"ACABAB"の場合の格納例を，図1に示す。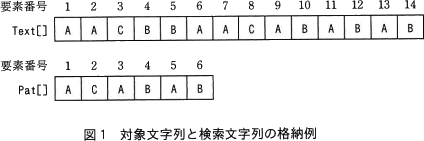
    pm08_1.png
  • 関数 BitapMatch は，関数 GenerateBitMask を呼び出す。
    関数 GenerateBitMask は，文字"A"～"Z"の文字ごとに，検索文字列に応じたビット列(以下，ビットマスクという)を生成し，要素数26の16ビット論理型配列 Mask[] に格納する。Mask[1] には文字"A"に対するビットマスクを，Mask[2] には文字"B"に対するビットマスクを格納する。このように Mask[1]～Mask[26] に文字"A"～"Z"に対応するビットマスクを格納する。
    関数 GenerateBitMask は，Mask[] の全ての要素を"0"Bに初期化した後，1以上で Pat[] の文字数以下の全てのiに対して，Pat[i] の文字に対応する Mask[] の要素である Mask[Index(Pat[i])] に格納されている値の，下位から数えてi番目のビットの値を1にする。
    関数 Index は，引数にアルファベット順でn番目の英大文字を設定して呼び出すと，整数n(1≦n≦26)を返す。
  • 図1で示した，Pat[] が"ACABAB"の例の場合，関数 GenerateBitMask を実行すると，Mask[] は図2のとおりになる。
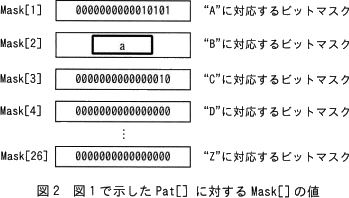
    pm08_2.png
  • 関数 GenerateBitMask の引数と返却値の仕様は，表1のとおりである。
    pm08_3.png
pm08_4.png
広告

設問1

プログラムの説明及びプログラム1中の　に入れる正しい答えを，解答群の中から選べ。
a に関する解答群
  • 0000000000000101
  • 0000000000101000
  • 0001010000000000
  • 1010000000000000
b に関する解答群
  • "0"B
  • "1"B
  • "1"BをPatLenビットだけ論理左シフトした値
  • "1"Bを(PatLen－1)ビットだけ論理左シフトした値
  • "1111111111111111"B
c に関する解答群
  • "1"Bを(i－1)ビットだけ論理左シフトした値
  • "1"Bをiビットだけ論理左シフトした値
  • "1"Bを(PatLen－1)ビットだけ論理左シフトした値
  • "1"BをPatLen ビットだけ論理左シフトした値
  • "1"B
解答選択欄
  • a:
  • b:
  • c:
  • a=イ
  • b=ア
  • c=ア

解説

〔aについて〕
関数 GenerateBitMask は、Pat[] に格納されている検索文字列の各文字について、その文字に対応するマスクの下位から数えてiビット目を1にします。この説明だと少しわかりにくいので、実際に図1の"ACABAB"がどのように変換されているかを図2で確認します。
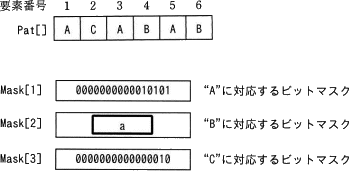
pm08_10.png
この関係をよく見ると、"A"に対応するビットマスクである Mask[1] は下位から数えて1、3、5番目、"C"に対応するビットマスクである Mask[3] は下位から数えて2番目のビットが1になっています。これは、Pat[] 内での文字の出現位置(要素番号)と一致します。
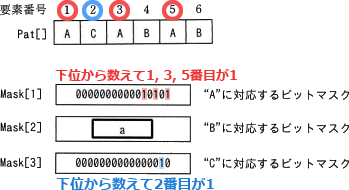
pm08_11.png
"B"は Pat[] の要素番号4と6に格納されているので、Mask[2] のビットは下位から数えて4番目と6番目のビットを1とした「0000000000101000」になると判断できます。

∴a＝イ：0000000000101000

〔bについて〕
ループ処理を通じて Mask[] の全要素（Mask[1]からMask[26]）に格納する値です。
本文中で「関数 GenerateBitMask は，Mask[] の全ての要素を"0"Bに初期化した後，…」と説明されていること、及びコメント部に/* 初期化 */とあることから、ここで Mask[] の全要素に格納する値は「"0"B」であると判断できます。

∴b＝ア："0"B

〔cについて〕
この処理では、本文中に説明されている「Mask[Index(Pat[i])] に格納されている値の，下位から数えてi番目のビットの値を1にする」を行っています。Mask[Index(Pat[i])は、現在処理中の文字(Pat[i])に対応するビットマスクを格納しています。ビットマスクの下位からi番目のビットを1にしたいので、iに応じて"1"Bを左に論理左シフトさせた値と論理和をとった結果でビットマスクを更新することになります。

具体的に言うと、Pat[]で1文字目の場合には下位から1ビット目を1にしたいので"1"Bと論理和をとり、2文字目の場合には下位から2ビット目を1にしたいので"10"Bと論理和をといった感じになります。つまり、文字の位置と論理和をとるビット列は次のように対応します。
  • 1文字目 → 下位から1ビット目を1にする → "1"B
  • 2文字目 → 下位から2ビット目を1にする → "10"B
  • 3文字目 → 下位から3ビット目を1にする → "100"B
  • 4文字目 → 下位から4ビット目を1にする → "1000"B
この関係を見ると、1文字目では"1"Bそのまま、2文字目では"1"Bを1ビット論理左シフトした値、3文字目では"1"Bを2ビット論理左シフトした値、…というように、"1"Bを(文字の位置－1)ビットだけ論理左シフトしたものであるとわかります。プログラム上、現在処理中の要素が何文字目かはiが保持していますから、Mask[Index(Pat[i])] と論理和をとるのは"1"Bを(i－1)ビットだけ論理左シフトした値が適切です。

∴c＝ア："1"Bを(i－1)ビットだけ論理左シフトした値
広告
〔関数 BitapMatch の説明〕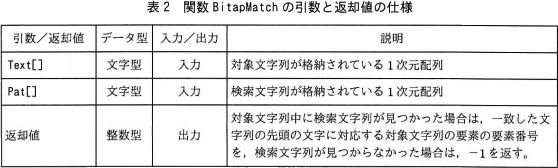
  • Text[] と Pat[] を受け取り，Text[] の要素番号の小さい方から Pat[] と一致する文字列を検索し，見つかった場合は，一致した文字列の先頭の文字に対応する Text[] の要素の要素番号を返し，見つからなかった場合は，－1を返す。
  • 図1の例では，Text[7]～Text[12] の文字列が Pat[] と一致するので，7を返す。
  • 関数 BitapMatch の引数と返却値の仕様は，表2のとおりである。
pm08_5.png
pm08_6.png

設問2

次の記述中の　に入れる正しい答えを，解答群の中から選べ。

　図1で示したとおりに，Text[] と Pat[] に値を格納し，関数 BitapMatch を実行した。プログラム2の行βを実行した直後の変数iと配列要素 Mask[Index(Text[i])] と変数 Status の値の遷移は，表3のとおりである。
　例えば，iが1のときに行βを実行した直後の Status の値は"1"Bであることから，iが2のときに行αを実行した直後の Status の値は，"1"Bを1ビットだけ論理左シフトした"10"Bと"1"Bとのビットごとの論理和を取った"11"Bとなる。次に，iが2のときに行βを実行した直後の Status の値は，Mask[Index(Text[2])] の値が"10101"Bであることを考慮すると，dとなる。
　同様に，iが8のときに行βを実行した直後の Status の値が"10"Bであるということに留意すると，iが9のときに行αを実行した直後の行βで参照する Mask[Index(Text[9])] の値はeであるので，行βを実行した直後の Status の値はfとなる。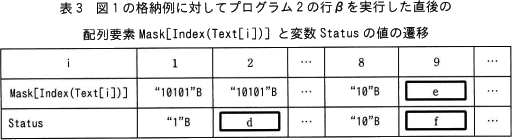
pm08_7.png
d，e，f に関する解答群
  • "0"B
  • "1"B
  • "10"B
  • "11"B
  • "100"B
  • "101"B
  • "10101"B
解答選択欄
  • d:
  • e:
  • f:
  • d=イ
  • e=キ
  • f=カ

解説

〔dについて〕
βの処理では、Status と Mask[Index(Text[i])] の論理積の結果で Status を更新します。
設問中に「iが2のときに行αを実行した直後の Status の値は…"11"Bとなる」及び「Mask[Index(Text[2])] の値が"10101"Bである」と記載されているので、この2つのビット列の論理積を求めます。※論理積は2つのビットがともに1のときにだけ1を出力する論理演算です。
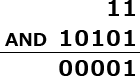
pm08_12.png
β処理後の Status の値は「"1"B」となります。

∴d＝イ："1"B

〔eについて〕
Mask[Index(Text[9])] が何を指しているのかを考えます。

図1で Text[9] を確認すると"A"です。関数 Index は引数の英大文字のアルファベット順を返すので、Index(A)は1を返します。したがって Mask[Index(Text[9])] は、"A"に対応するビットマスクであるMask[1]を参照することになります。Mask[1] の値は図2より「"10101"B」とわかります。

∴e＝キ："10101"B

〔fについて〕
設問中に「iが8のときに行βを実行した直後の Status の値が"10"Bである」とあるので、この値をもとにiが9のときのα、βの処理を行って結果を求めます。

[iが9のときのαの処理]
Status の値を1ビットだけ論理左シフトした値："100"B
"100"Bと"1"Bの論理和："101"B

[iが9のときのβの処理]
Status の値："101"B
Mask[Index(Text[9])]の値："10101"B
"101"Bと"10101"Bの論理積："101"B
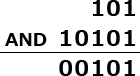
pm08_13.png
β処理後の Status の値は「"101"B」となります。

∴f＝カ："101"B
広告

設問3

関数 GenerateBitMask の拡張に関する，次の記述中の　に入れる正しい答えを，解答群の中から選べ。ここで，プログラム3中のbには，設問1のbの正しい答えが入っているものとする。

　表4に示すような正規表現を検索文字列に指定できるように，関数 GenerateBitMask を拡張し，関数 GenerateBitMaskRegex を作成した。
pm08_8.png
pm08_9.png
　Pat[] に"AC[BA]A[ABC]A"を格納して，関数 GenerateBitMaskRegex を呼び出した場合を考える。この場合，文字"A"に対応するビットマスクである Mask[1] はgとなり，関数 GenerateBitMaskRegex の返却値はhとなる。また，Pat[] に格納する文字列中において[]を入れ子にすることはできないが，誤って Pat[] に"AC[B[AB]AC]A"を格納して関数 GenerateBitMaskRegex を呼び出した場合，Mask[1]はiとなる。
g，i に関する解答群
  • "1001101"B
  • "1010100001"B
  • "1011001"B
  • "101111"B
  • "110011"B
  • "111101"B
h に関する解答群
  • 4
  • 6
  • 9
  • 13
解答選択欄
  • g:
  • h:
  • i:
  • g=カ
  • h=イ
  • i=ウ

解説

〔gについて〕
[]は、その内部に記載されている文字のいずれか1文字に一致する文字を表すので、"AC[BA]A[ABC]A"は6文字のパターンを表していることになります（3, 5文字目が正規表現）。
pm08_14.png
"A"が出現するのは1, 3, 4, 5, 6文字目なので、Mask[1]は下位から1, 3, 4, 5, 6ビット目を1にした「"111101"B」になります。

∴g＝カ："111101"B

〔hについて〕
関数 GenerateBitMaskRegex の返却値である PatLen はプログラム中の2か所に加算処理が記述されています。1つ目は"["を見つけたとき、2つ目は Mode が0のときです。Mode は正規表現[]の内側を処理していることを示すフラグで、正規表現の先頭文字である"["を見つけると1になり、正規表現の終端文字である"]"に達すると0になります。つまり、2つ目のModeが0のときとは、正規表現ではない普通の文字のときであると判断できます。

このルールに従って"AC[BA]A[ABC]A"で PatLen が加算される部分を考えると以下の6か所があることがわかります。
pm08_15.png
したがって、関数 GenerateBitMaskRegex の返却値は「6」になります。

∴h＝イ：6

〔iについて〕
プログラムをトレースして答えを導きます。PatLen が加算される箇所を確実に把握しておくことがポイントとなります。Mask[1] 以外の Mask[] を更新する処理は関係ないので割愛しています。
1文字目 A
PatLen ← 1
Mask[1]の値："0"B
"1"Bを(1－1)ビットだけ論理左シフトした値："1"B
Mask[1] ← "0"Bと"1"Bの論理和＝"1"B
2文字目 C
PatLen ← 2
3文字目 [
PatLen ← 3
Mode ← 1
4文字目 B
5文字目 [
PatLen ← 4
Mode ← 1
6文字目 A
Mask[1]の値："1"B
"1"Bを(4－1)ビットだけ論理左シフトした値："1000"B
Mask[1] ← "1000"Bと"1"Bの論理和＝"1001"B
7文字目 B
8文字目 ]
Mode ← 0
9文字目 A
PatLen ← 5
Mask[1]の値："1001"B
"1"Bを(5－1)ビットだけ論理左シフトした値："10000"B
Mask[1] ← "10000"Bと"1001"Bの論理和＝"11001"B
10文字目 C
PatLen ← 6
11文字目 ]
Mode ← 0
12文字目 A
PatLen ← 7
Mask[1]の値："11001"B
"1"Bを(7－1)ビットだけ論理左シフトした値："1000000"B
Mask[1] ← "1000000"Bと"11001"Bの論理和＝"1011001"B
これで Pat[] の全要素を処理したので終了、Mask[1] には「"1011001"B」が格納されています。

∴i＝ウ："1011001"B
広告
広告

前の問題次の問題

▲
Pagetop