令和元年秋期試験問題 午前問1

問1解説へ
次の流れ図は,10進整数 j(0<j<100) を8桁の2進数に変換する処理を表している。2進数は下位桁から順に,配列の要素 NISHIN(1) から NISHIN(8) に格納される。流れ図のa及びbに入る処理はどれか。ここで,j div 2 はjを2で割った商の整数部分を,j mod 2 はjを2で割った余りを表す。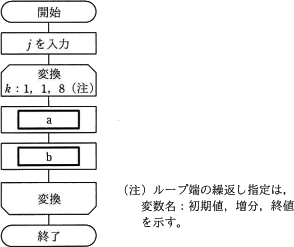


広告
解説
10進数から2進数に変換する方法として 2 で割ることを繰り返すものがありますが、本問の流れ図は、この方法をアルゴリズムとして表したものです。
例として j=50 のときに各配列要素に格納される値の違いを見ていきましょう。NISHIN[1] が最下位ビット(一番右)、NISHIN[8] が最上位ビット(一番左)で下位ビットから順番に値を格納していきます。
10進数 50 は「32+16+2=25+24+21」ですから、2進数8ビットだと 0011 0010 と表せます。流れ図の処理でも、aとbを繰り返して同様に変換されるかどうかを確認していくことで、正しい解を導きます。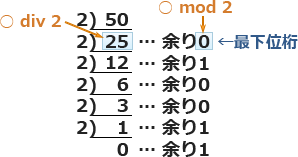
例として j=50 のときに各配列要素に格納される値の違いを見ていきましょう。NISHIN[1] が最下位ビット(一番右)、NISHIN[8] が最上位ビット(一番左)で下位ビットから順番に値を格納していきます。
10進数 50 は「32+16+2=25+24+21」ですから、2進数8ビットだと 0011 0010 と表せます。流れ図の処理でも、aとbを繰り返して同様に変換されるかどうかを確認していくことで、正しい解を導きます。
- [a] 50 div 2 = 25 → j右から1ビット目が 0 ではないので誤り。
[b] 25 mod 2 = 1 → NISHIN[1] - [a] 50 mod 2 = 0 → jj が 0 になり、配列要素に格納されるのがすべて 0 になってしまうので誤り。
[b] 0 div 2 = 0 → NISHIN[1]
[a] 0 mod 2 = 0 → j
[b] 0 div 2 = 0 → NISHIN[2]
(以降繰り返し) - [a] 50 div 2 = 25 → NISHIN[1]最下位桁の NISHIN[1] の値が25になってしまいます。2進数に変換する処理なので NISHIN(1) から NISHIN(8) に格納されるのは 0 または 1 でなくてはなりません。
[b] 25 mod 2 = 1 → j - 正しい処理です。最後まで流れを見ていきましょう。[a] 50 mod 2 = 0 → NISHIN[1]この時点で k が8になりループが終了します。NISHIN(1)が最下位桁、NISHIN(8)が最上位桁ですから、上位桁から順番に 0011 0010 が格納されていることになります。
[b] 50 div 2 = 25 → j
[a] 25 mod 2 = 1 → NISHIN[2]
[b] 25 div 2 = 12 → j
[a] 12 mod 2 = 0 → NISHIN[3]
[b] 12 div 2 = 6 → j
[a] 6 mod 2 = 0 → NISHIN[4]
[b] 6 div 2 = 3 → j
[a] 3 mod 2 = 1 → NISHIN[5]
[b] 3 div 2 = 1 → j
[a] 1 mod 2 = 1 → NISHIN[6]
[b] 1 div 2 = 0 → j
[a] 0 mod 2 = 0 → NISHIN[7]
[b] 0 div 2 = 0 → j
[a] 0 mod 2 = 0 → NISHIN[8]
[b] 0 div 2 = 0 → j

広告