分野：テクノロジ系
中分類：アルゴリズムとプログラミング
小分類：アルゴリズム

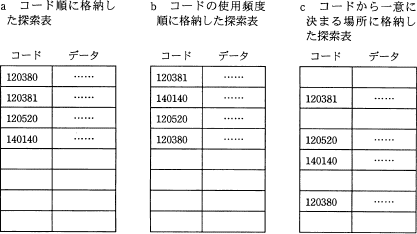
[a コード順に格納した探索表]
線形探索では、(N+1)/2 回, 二分探索法では [log₂N] 回が平均探索回数となります。([a]はaを超えない最大の整数を表します。)
データが昇順または降順に整列されている場合は、線形探索よりも二分探索の平均計算量が小さくなります。

[b コードの使用頻度順に格納した探索表]
使用頻度が高いデータが探索表の先頭のほうにたくさんあることになります。線形探索では探索表の先頭から順番に探索していくので、このような探索表では有効な方式です。
２分探索法は、データが整列されていないと使えないという条件がありますし、この表はハッシュ法に対応していないので、線形探索が唯一使用できる方法となります。

[c コードから一意に決まる場所に格納した探索表]
ハッシュ法は、探索データのキー値から、そのデータの格納場所（アドレス）を直接計算する方法で、(シノニムが発生しなければ)１回の計算で一意に目的のデータにたどりつくことができます。
１回の探索でいいので、この探索表の場合、最も計算量が少ない探索法はハッシュ表探索です。

まとめると、a が２分探索、b が線形探索、c がハッシュ表探索となります。