令和2年免除試験問題 問63

問63解説へ
投資効果を正味現在価値法で評価するとき,最も投資効果が大きい(又は損失が小さい)シナリオはどれか。ここで,期間は3年間,割引率は5%とし,各シナリオのキャッシュフローは表のとおりとする。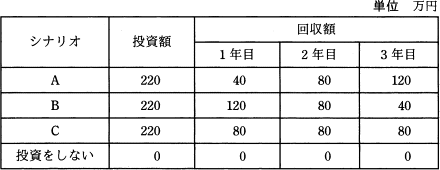

- A
- B
- C
- 投資をしない
広告
解説
正味現在価値法は、一定期間のキャッシュフローを、時間的変化に割引率を設定して現在価値に換算した上で、キャッシュフローの合計値を求め、その大小で評価する手法です。
例えば割引率5%とすると、1年後に受け取る100万円は「100万円÷1.05」、2年後に受け取る100万円は「100万円÷1.052」、n年後に受け取る100万円は「100万円÷1.05n」という具合に現在価値に換算します。つまり、同じ100万円でも将来に受け取るほどその価値を低く見積もります。
本来でしたらシナリオごとに具体的な計算を行うのですが、この計算はなかなか骨の折れる作業です。そこで、本問では各シナリオの回収額の合計が同じになっています。上記の理屈を踏まえると、回収合計額が同じならば、より早く大きな金額を受け取れた方が現在価値の合計が高くなるはずです。
したがって、3つのシナリオを現在価値が高くなる順に並べると、1年目の割合が高いB、3年間に平準化されているC、最終年の割合が多いAの順になります。
最後に、現在価値が投資額を上回っているかどうかについても検討しなければなりません。「現在価値<投資額」ならば、投資価値がないと判断されるからです。よって、シナリオBの現在価値を概算で求めます。
120÷1.05+80÷1.052+40÷1.053
≒120÷1.05+80÷1.1+40÷1.15
≒114.2+72.7+34.7
=221.6(万円)
少額ではありますが投資額の220万円を上回るので、投資をしない案よりもシナリオBの方が有利と判断されます。
例えば割引率5%とすると、1年後に受け取る100万円は「100万円÷1.05」、2年後に受け取る100万円は「100万円÷1.052」、n年後に受け取る100万円は「100万円÷1.05n」という具合に現在価値に換算します。つまり、同じ100万円でも将来に受け取るほどその価値を低く見積もります。
本来でしたらシナリオごとに具体的な計算を行うのですが、この計算はなかなか骨の折れる作業です。そこで、本問では各シナリオの回収額の合計が同じになっています。上記の理屈を踏まえると、回収合計額が同じならば、より早く大きな金額を受け取れた方が現在価値の合計が高くなるはずです。
したがって、3つのシナリオを現在価値が高くなる順に並べると、1年目の割合が高いB、3年間に平準化されているC、最終年の割合が多いAの順になります。
最後に、現在価値が投資額を上回っているかどうかについても検討しなければなりません。「現在価値<投資額」ならば、投資価値がないと判断されるからです。よって、シナリオBの現在価値を概算で求めます。
120÷1.05+80÷1.052+40÷1.053
≒120÷1.05+80÷1.1+40÷1.15
≒114.2+72.7+34.7
=221.6(万円)
少額ではありますが投資額の220万円を上回るので、投資をしない案よりもシナリオBの方が有利と判断されます。
//実際に計算してみると各シナリオの現在価値は以下の額になりました。
var x = 1.05;
//A
40/x+80/(x*x)+120/(x*x*x)=214.3181081956592
//B
120/x+80/(x*x)+40/(x*x*x)=221.4015765036173
//C
80/x+80/(x*x)+80/(x*x*x)=217.85984234963826
var x = 1.05;
//A
40/x+80/(x*x)+120/(x*x*x)=214.3181081956592
//B
120/x+80/(x*x)+40/(x*x*x)=221.4015765036173
//C
80/x+80/(x*x)+80/(x*x*x)=217.85984234963826
広告