令和5年免除試験問題 問41

問41解説へ
図に示すとおりに作業を実施する予定であったが,作業Aで1日の遅れが生じた。各作業の費用増加率を表の値とするとき,当初の予定日数で終了するために掛かる増加費用を最も少なくするには,どの作業を短縮すべきか。ここで,費用増加率とは,作業を1日短縮するのに要する増加費用のことである。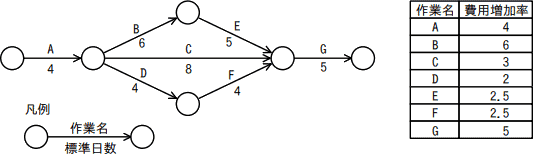

- B
- C
- D
- E
広告
解説
アローダイアグラムの問題なので、まずは当初計画のスケジュールにおけるクリティカルパスを求めます。
設問では作業Aが1日遅れたとあります。作業Aはクリティカルパス上の作業ですから、このままだとプロジェクト全体でも1日遅れてしまうことになります。この遅れを取り戻すには、同じくクリティカルパス上の作業を1日短縮する必要があります。
残るクリティカルパス上の作業はB、E、Gなので、この3つの作業の費用増加率を比べると、費用増加率はB=6、E=2.5、G=5と、作業Eが最も少ないです。したがって、増加費用を最も少なくするためには作業Eを短縮することになります。
- A→B→E→G
- 4+6+5+5=20日
- A→C→G
- 4+8+5=17日
- A→D→F→G
- 4+4+4+5==17日
設問では作業Aが1日遅れたとあります。作業Aはクリティカルパス上の作業ですから、このままだとプロジェクト全体でも1日遅れてしまうことになります。この遅れを取り戻すには、同じくクリティカルパス上の作業を1日短縮する必要があります。
残るクリティカルパス上の作業はB、E、Gなので、この3つの作業の費用増加率を比べると、費用増加率はB=6、E=2.5、G=5と、作業Eが最も少ないです。したがって、増加費用を最も少なくするためには作業Eを短縮することになります。
広告