平成17年秋期試験問題 午前問1
広告
解説
10進数の小数部をN進数の小数に変換する方法の一つとして、10進小数に基数Nを掛けて演算結果の整数部を取り出し、さらに演算結果の小数部に基数Nを掛けて整数部を取り出して…と繰り返すものがあります。この計算過程で小数部が0になれば有限小数であると言えます。
例えば10進小数 0.8125 を8進小数にするには以下のように計算します。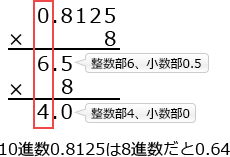 この方法を用いて各10進小数が8進数の有限小数になるかどうかを確認します。
この方法を用いて各10進小数が8進数の有限小数になるかどうかを確認します。
a1×8-1+a2×8-2+a3×8-3+・・・+an×8-n
のようになっていて、これを8倍すると、8-1→80 で、最初の項が整数になります。他の項も、8-2→8-1 のようにひとつ上がっていきます。これを繰り返すと、8-n の項は8をn回掛けた時点で整数になります。つまり、有限桁であれば何回目かで小数部分がなくなります。
例えば10進小数 0.8125 を8進小数にするには以下のように計算します。

- 0.3×8=2.4
0.4×8=3.2
0.2×8=1.6
0.6×8=4.8
0.8×8=6.4
小数部が再び0.4になり、後は無限に繰り返すことになるので無限小数(0.23146(8))です。 - 0.4×8=3.2
0.2×8=1.6
0.6×8=4.8
0.8×8=6.4
小数部が再び0.4になり、後は無限に繰り返すことになるので無限小数(0.3146(8))です。 - 正しい。0.5×8=4.0 と小数部が0になるので有限小数(0.4(8))です。
- 0.8×8=6.4
0.4×8=3.2
0.2×8=1.6
0.6×8=4.8
小数部が再び0.8になり、後は無限に繰り返すことになるので無限小数(0.6314(8))です。
a1×8-1+a2×8-2+a3×8-3+・・・+an×8-n
のようになっていて、これを8倍すると、8-1→80 で、最初の項が整数になります。他の項も、8-2→8-1 のようにひとつ上がっていきます。これを繰り返すと、8-n の項は8をn回掛けた時点で整数になります。つまり、有限桁であれば何回目かで小数部分がなくなります。
広告