平成17年春期試験問題 午前問7

問7解説へ
次の図は,ある地方の日単位の天気の移り変わりを示したものであり,数値は翌日の天気の変化の確率を表している。ある日の天気が雨のとき,2日後の天気が晴れになる確率は幾らか。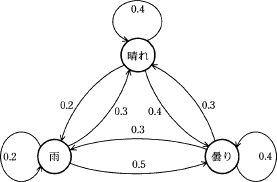

- 0.15
- 0.27
- 0.3
- 0.33
広告
解説
この設問の例のように未来の挙動が現在の値だけで決定され、過去の挙動と無関係であるという性質を持つ確率過程のことをマルコフ過程といいます。
雨の日の2日後が晴れであるときには、
そして2日後が晴れである確率は、この3つの過程が発生する確率を足し合わせたものになります。
各過程の起こる確率は、
0.12+0.15+0.06=0.33
したがって図の条件で雨の日の2日後が晴れである確率は0.33であるとわかります。
雨の日の2日後が晴れであるときには、
- 雨→晴れ→晴れ
- 雨→曇り→晴れ
- 雨→雨 →晴れ
そして2日後が晴れである確率は、この3つの過程が発生する確率を足し合わせたものになります。
各過程の起こる確率は、
- [晴れ→晴れ]0.3×0.4=0.12
- [曇り→晴れ]0.5×0.3=0.15
- [雨→晴れ]0.2×0.3=0.06
0.12+0.15+0.06=0.33
したがって図の条件で雨の日の2日後が晴れである確率は0.33であるとわかります。
広告