平成17年春期試験問題 午前問9

問9解説へ
8ビットのビット列の下位4ビットが変化しない操作はどれか。
- 16進表記 0F のビット列との論理積をとる。
- 16進表記 0F のビット列との論理和をとる。
- 16進表記 0F のビット列との排他的論理和をとる。
- 16進表記 0F のビット列との否定論理積をとる。
広告
解説
各論理演算は次のような操作を意味しています。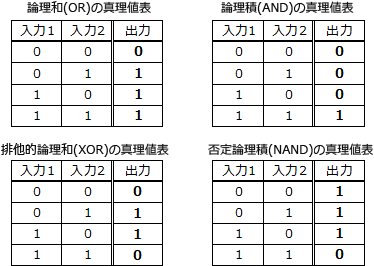 16進表記 0F は2進表記で「00001111」です。この「00001111」と8ビットのビット列に対して、それぞれの論理演算を行うことで正解を導きます。ここでは演算対象となる8ビットのビット列に、上位4ビットと下位4ビットそれぞれで1と0の変化が把握しやすい「10101010」を用いています。
16進表記 0F は2進表記で「00001111」です。この「00001111」と8ビットのビット列に対して、それぞれの論理演算を行うことで正解を導きます。ここでは演算対象となる8ビットのビット列に、上位4ビットと下位4ビットそれぞれで1と0の変化が把握しやすい「10101010」を用いています。
一般に任意のビット列から特定のビット列を取り出したいときにはAND演算、任意のビット列のうち特定のビット列を反転させたいときにはXOR演算を使うことができるので覚えておきましょう。
- 論理積(AND)
- 2つのビットが両方とも1のときにだけ1を出力し、それ以外は0を出力する。
- 論理和(OR)
- 2つのビットのどちらかが1であれば1を出力し、両方とも0のときは0を出力する。
- 排他的論理和(XOR)
- 2つのビットが異なるときは1を出力し、同じときは0を出力する。
- 否定論理積(NAND=Not AND)
- AND演算の結果を反転した演算で、2つのビットが両方とも1のときにだけ0を出力し、それ以外は1を出力する。

- 10101010 AND 00001111=00001010
- 10101010 OR 00001111=10101111
- 10101010 XOR 00001111=10100101
- 10101010 NAND 00001111=11110101
一般に任意のビット列から特定のビット列を取り出したいときにはAND演算、任意のビット列のうち特定のビット列を反転させたいときにはXOR演算を使うことができるので覚えておきましょう。
広告