平成19年秋期試験問題 午前問15

問15解説へ
整数x,y(x>y≧0)に対して,次のように定義された関数F(x,y)がある。F(231,15)の値は幾らか。ここで,x mod y はxをyで割った余りである。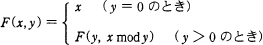
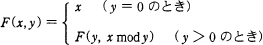
- 2
- 3
- 5
- 7
広告
解説
「y>0 のとき F(x,y) = F(y,x mod y) 」と決められているということは、左辺を右辺の形に変換できるということです。すなわち、右辺の第1引数には左辺の第2引数(y)を与え、右辺の第2引数には x mod y を与えて計算すればよいわけです。
最初の F(231,15) … x=231、y=15の場合、231 mod 15 = 6 ですから F(231,15) = F(15,6) です。これを繰り返しながら最終的な値を求めていきます。
F(231,15)
=F(15,231 mod 15)=F(15,6)
=F(6,15 mod 6)=F(6,3)
=F(3,6 mod 3)=F(3,0)
=3
したがって正解は「3」になります。
最初の F(231,15) … x=231、y=15の場合、231 mod 15 = 6 ですから F(231,15) = F(15,6) です。これを繰り返しながら最終的な値を求めていきます。
F(231,15)
=F(15,231 mod 15)=F(15,6)
=F(6,15 mod 6)=F(6,3)
=F(3,6 mod 3)=F(3,0)
=3
したがって正解は「3」になります。
広告