平成21年秋期試験午後問題　問8(データ構造及びアルゴリズム)

平成21年秋期試験午後問題　問8

問8　データ構造及びアルゴリズム

次のアルゴリズムの説明及びプログラムを読んで，設問に答えよ。

　方程式の解の一つを求めるアルゴリズムである。任意に定めた解の予測値から始めて，計算を繰り返しながらその値を真の値に近づけていく。この方法は，ニュートン法と呼ばれる。

〔アルゴリズム1の説明〕
　3次方程式 a₃x³＋a₂x²＋a₁x＋a₀＝0 の解の一つを，次の手順で求める。

解の予測値 x，係数 a₃，a₂，a₁，a₀ を読み込む
3×a₃をb₂に，2×a₂の値をb₁に，1×a₁の値をb₀に，それぞれ求める。
次の①～④の処理を一定の回数繰り返す。
1. a₃x³＋a₂x²＋a₁x＋a₀ の値を求め，これを f とする。
2. b₂x²＋b₁x＋b₀ の値を求め，これを d とする。
3. x，f，dの値を印字する。
4. x－ƒdの値(解の一つにより近い値となる)を求め，これを新たな x とする。

　プログラム1は，このアルゴリズム1を実装したものである。

〔アルゴリズム2の説明〕
　アルゴリズム1を一般化して，n次方程式 a_nxⁿ＋a_n-1x^n-1＋…＋a₁x＋a₀＝0 の解の一つを，次の手順で求める。
　なお，方程式によっては解が求められない場合がある。

次数n，解の予測値x，係数a_n，a_n-1，…，a_1, a₀ を読み込む。
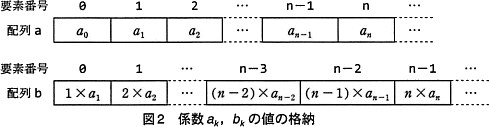
n×a_n の値を b_n-1に，(n－1)×a_n-1 の値を b_n-2に，…，2×a₂ の値をb₁に，1×a₁の値をb₀に，それぞれ求める。
次の①～④の処理を一定の回数繰り返す。
1. a_nxⁿ＋a_n-1x^n-1＋…＋a₁x＋a₀ の値を求め，これを f とする。
2. b_n-1x^n-1＋b_n-2x^n-2＋…＋b₁x＋b₀ の値を求め，これを d とする。
3. x，f，dの値を印字する。
4. x－ƒdの値(解の一つにより近い値となる)を求め，これを新たな x とする。

　プログラム2は，このアルゴリズム2を実装したものである。

設問

次の記述中の　に入れる正しい答えを，解答群の中から選べ。

解の予測値 x＝2.5，係数 a₃＝1，a₂＝－3，a₁＝－1，a₀＝3 を与えて，3次方程式 x³－3x²－x＋3＝0 の解の一つを求める(解は3，1，－1)。プログラム1を有る処理系で実行した結果，図1に示す通り解の一つであるx＝3が近似的に得られた。
　この印字結果の行番号6，7のxの値(網掛けの部分)はいずれも3.000000である。行番号6，7を印字した時点で変数xに保持されていた実際の値をそれぞれ x_6, x₇ で表すと，a。
　なお，この処理系では，実数型は2進数の浮動小数点形式であって，有効けた数は10進数で十数けた程度であることが分かっている。
プログラム2では，係数 a_k (k：n，n－1，…，1，0)の値を配列 a の要素 a[k] に，b_k (k：n－1，n－2，…，1，0)の値を配列 b の要素 b[k] に，それぞれ図2のように格納している。
　プログラム2の行番号9～11は，アルゴリズム2の手順(2)の処理である。この部分のプログラムは，次のようになる。
　また，行番号13～18は，アルゴリズム2の手順(3)の①と②の処理である。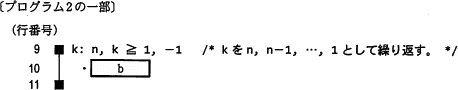
プログラム1では，例えばfの値a₃ｘ³＋a₂ｘ²＋a₁ｘ＋a₀を求める式を，

　　ｆ←((a3×x＋a2)×x＋a1)×x＋a0

と変形して，演算回数を減らす工夫をしている。この部分にも同様の工夫をすると，プログラムは次のようになる。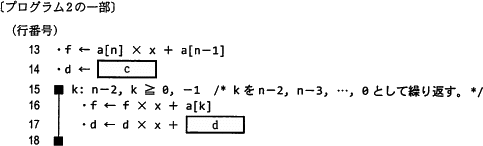
次数n＝4，係数a₄＝1，a₃＝－8，a₂＝24，a₁＝－32，a₀＝16として，4次方程式 x⁴－8x³＋24x²－32x＋16＝0 の解を求める(4個の解がすべて2)。解の予測値をx＝2.00001として，ある処理系でプログラム2を実行したところ，図3に示すとおりの印字結果となった。
　この印字結果の行番号2では，xの値(網掛けの部分)が解である2から遠ざかってしまっている。その原因を調べるため，f を求める式に実際の数値を当てはめて，
として，(A)の部分の中間結果を印字するプログラムを作り，同じ処理系で実行した。印字結果は－16.00000であり，正確な値－15.99999999999999999999と有効数字7けたで一致した。しかし，行番号1で印字された f の値は，正確な値である10^-20(印字の表記では1.000000(－20))とは異なっている。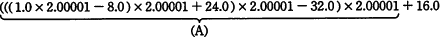
　これらのことから判断して，(A)の部分では演算の過程でeが徐々に累積し，(A)の計算結果に16.0を加算するときに，けた落ちが発生したと考えられる。