分野：テクノロジ系
中分類：基礎理論
小分類：離散数学

最短で答えを導く方法は論理式にド・モルガンの法則を適用して変形することです。

ド・モルガンの法則

A＋B＝A・B
A・B＝A＋B

この場合の解法は以下のようになります。

　(A＋B)・(A＋C)
＝(A＋B)＋(A＋C)
＝A・B＋A・C

この変形により問題文の論理式は「A・B+A・C」と等しいことがわかります。

また地道にベン図を描いて比較していく方法でも解いてみます。

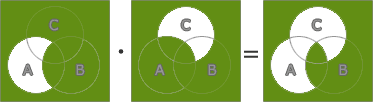
最初に(A＋B)・(A＋C)の表す集合をベン図で描いてみます。
(A+B)・(A+C)は以下のようになります。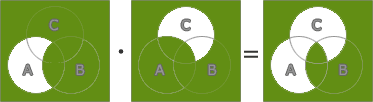さらに設問の論理式は上図で求めた集合の補集合であるので、となります。

さらに各選択肢の論理式についてもベン図を描いてみます。

• A・B+A・C
  
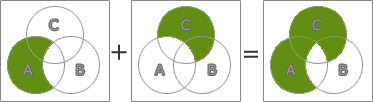
• A・B+A・C
  
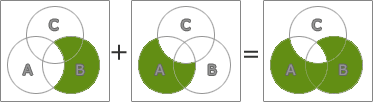
• (A+B)・(A+C)
  
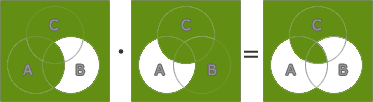
• (A+B)・(A+C)
  
  

これらのベン図を問題文の論理式が表すベン図と比較すると、やはり「ア」の論理式と等価であることがわかります。