平成24年秋期試験午後問題 問8

問8 データ構造及びアルゴリズム
次のプログラムの説明及びプログラムを読んで,設問に答えよ。
鉄道の路線がある。駅数 N は2以上で,各駅には駅番号(1,2,…,N)が付いている。どの任意の2駅間にも,それらを結ぶ経路が一つ以上存在する。また,隣接する2駅間を直接結ぶ経路は一つだけ存在し,その距離が与えられている。図1に5駅からなる鉄道の路線例を示す。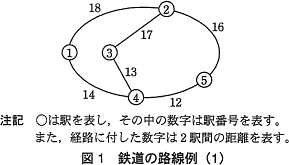 〔プログラムの説明〕
〔プログラムの説明〕
副プログラム CalcDist は,駅数N及び要素数N×Nの2次元配列 Dist を受け取り,プログラムに示すアルゴリズム(Warshall-Floyd法)によって,配列 Dist の内容を更新しながら各駅間の最短距離を求めていく。実行が終わると,任意の2駅 i,j 間の最短距離が Dist[i][j] に求められている。どの2駅間についても,その最短距離は 999 より小さいものとする。配列 Dist の添字は1から始まる。
副プログラム CalcDist に渡す配列 Dist には,次の値を格納する。
なお,図1の路線情報を格納した配列 Dist の内容を,図2の初期値に示してある。 図1の路線情報を配列 Dist に格納して,CalcDist を実行した。配列 Dist の内容の 変化を print(N,Dist) で印字した結果は,図2のとおりであった。
図1の路線情報を配列 Dist に格納して,CalcDist を実行した。配列 Dist の内容の 変化を print(N,Dist) で印字した結果は,図2のとおりであった。 駅数Nに関して,副プログラム CalcDist の計算量のオーダーはc,またメモリ使用量のオーダーはdである。そこで,駅数Nが大きい場合に,計算量やメモリ使用量を減らすための方法を考える。
駅数Nに関して,副プログラム CalcDist の計算量のオーダーはc,またメモリ使用量のオーダーはdである。そこで,駅数Nが大きい場合に,計算量やメモリ使用量を減らすための方法を考える。
例えば,配列 Dist の対称性に着目し,プログラム中の の部分を, とすれば,繰返し処理中の選択処理の実行回数を約半分に減らすことができる。
とすれば,繰返し処理中の選択処理の実行回数を約半分に減らすことができる。
次に,少ないメモリ使用量で,任意の2駅 i,j 間の最短距離を求める方法を考える。
駅を,乗換駅(3方向以上に隣接する駅がある),終端駅(1方向だけに隣接する駅がある),中間駅(2方向だけに隣接する駅がある)の3種類に分ける。乗換駅と終端駅を合わせて基幹駅と呼ぶ。基幹駅の数を K として,駅番号 1~K が基幹駅,駅番号 K+1~N が中間駅となるように駅番号を定める。ここで,K≧2であるとする。図3の路線例では,駅①~③が乗換駅,駅④が終端駅,駅⑤~⑩が中間駅である。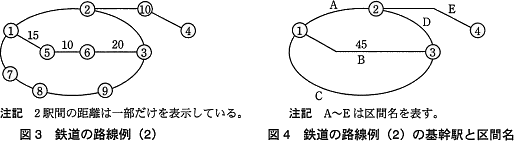 各駅間の最短距離は,次の方法で求める。
各駅間の最短距離は,次の方法で求める。
鉄道の路線がある。駅数 N は2以上で,各駅には駅番号(1,2,…,N)が付いている。どの任意の2駅間にも,それらを結ぶ経路が一つ以上存在する。また,隣接する2駅間を直接結ぶ経路は一つだけ存在し,その距離が与えられている。図1に5駅からなる鉄道の路線例を示す。

副プログラム CalcDist は,駅数N及び要素数N×Nの2次元配列 Dist を受け取り,プログラムに示すアルゴリズム(Warshall-Floyd法)によって,配列 Dist の内容を更新しながら各駅間の最短距離を求めていく。実行が終わると,任意の2駅 i,j 間の最短距離が Dist[i][j] に求められている。どの2駅間についても,その最短距離は 999 より小さいものとする。配列 Dist の添字は1から始まる。
副プログラム CalcDist に渡す配列 Dist には,次の値を格納する。
なお,図1の路線情報を格納した配列 Dist の内容を,図2の初期値に示してある。
- 2駅 i,j が隣接しているとき,Dist[i][j] 及び Dist[j][i] には,その駅間距離を格納する。例えば,図1の駅①と②は隣接しているので,Dist[1][2] 及び Dist[2][1] には,18を格納する。
- 2駅 i,j が隣接していないとき,Dist[i][j] 及び Dist[j][i] には,未確定を表す距離 999 を格納する。例えば,図1の駅①と③は隣接していないので,Dist[1][3] 及び Dist[3][1] には,999 を格納する。
- 各駅iについて,Dist[i][i] には0を格納する。


例えば,配列 Dist の対称性に着目し,プログラム中の の部分を,

次に,少ないメモリ使用量で,任意の2駅 i,j 間の最短距離を求める方法を考える。
駅を,乗換駅(3方向以上に隣接する駅がある),終端駅(1方向だけに隣接する駅がある),中間駅(2方向だけに隣接する駅がある)の3種類に分ける。乗換駅と終端駅を合わせて基幹駅と呼ぶ。基幹駅の数を K として,駅番号 1~K が基幹駅,駅番号 K+1~N が中間駅となるように駅番号を定める。ここで,K≧2であるとする。図3の路線例では,駅①~③が乗換駅,駅④が終端駅,駅⑤~⑩が中間駅である。

- 中間駅を全て除いて,基幹駅だけからなる路線を考え,二つの基幹駅を結ぶ経路ごとに一意の区間名を付ける。図3の路線例にこの操作を加えたものが図4である。例えば,図3の経路①-⑤-⑥-③は,図4の区間Bに対応する。
- 要素数 K×K の2次元配列 Dist を用意し,事前に配列 Dist に各基幹駅間の最短距離を求めておく。
- 全ての駅について,表1に示す形式の駅情報表を用意する(表1には,図3の駅情報の一部が示してある)。
中間駅の場合,Sec はその駅が属する区間の区間名,KL,KHはその駅が属する区間の両端の駅番号(KL ≦ KHとする),ToKL,ToKHはその駅から駅 KL,KH までの距離である。基幹駅の場合,その駅は自分自身の駅を両端とする距離0の区間に属すると考えて,表1の例のように中間駅と同様の情報を用意する。
これらの情報は,駅番号を添字として参照する。例えば,駅番号5のToKLの値はToKL[5] として参照する。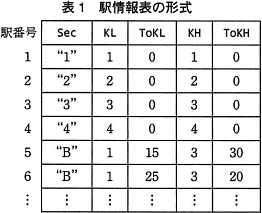
- 2駅 i,j 間の最短距離を求める。一般に,両駅が属する区間が異なる場合,駅iから駅jへ行く経路は,
(駅i)→(駅iが属する区間のいずれか一端の基幹駅)
→(駅jが属する区間のいずれか一端の基幹駅)→(駅j)
となる,したがって,次の式で求める4通りの値D1,D2,D3,D4のうちの最小値が,2駅 i,j 間の最短距離となる。- D1←ToKL[i]+Dist[KL[i]][KL[j]]+ToKL[j]
- D2←ToKL[i]+Dist[KL[i]][KH[j]]+ToKH[j]
- D3←ToKH[i]+Dist[KH[i]][KL[j]]+ToKL[j]
- D4←ToKH[i]+Dist[KH[i]][KH[j]]+ToKH[j]

広告
設問
本文中及び図2中の に入れる正しい答えを,解答群の中から選べ。
a,b に関する解答群
- 33
- 34
- 35
- 999
c,d に関する解答群
- O(N)
- O(NlogN)
- O(N2)
- O(N3)
e に関する解答群
- 1, to ≦ From, 1
- 1, to ≦ From + 1, 1
- From, To ≦ N - 1, 1
- From + 1, To ≦ N, 1
f に関する解答群
- (KL[i]=KL[j])and(KH[i]=KH[j])
- (KL[i] ≠KL[j])or(KH[i] ≠KH[j])
- Sec[i]=Sec[j]
- Sec[i] ≠Sec[j]
g に関する解答群
- 6
- 8
- 9
- 14
解答選択欄
- a:
- b:
- c:
- d:
- e:
- f:
- g:
- a=ウ
- b=ア
- c=エ
- d=ウ
- e=エ
- f=ウ
- g=ウ
解説
〔abについて〕問題文には副プログラム CalcDist について、「配列 Dist の内容を更新しながら各駅間の最短距離を求めていく」とだけ説明されていて、プログラムの具体的な動作については記述されてないのでプログラムのソースを見て動作を考える必要があります。
副プログラム CalcDist を見ると、三重ループを使い Via(経由)、From(起点)、To(終点)の全組合せについて処理を行っています。処理内容としては、現在の駅間最短距離(Dist[From][To])よりも経由駅を介した距離(Dist[From][Via] + Dist[Via][To])の方が小さくなるとき、配列 Dist の内容を更新しています。
図2で Dist の変化を確認すると、初期値から Via=1 のループ終了後では From=2、To=4 および From=4、To=2 の部分が、未確定を表す999から32に更新されています。

これを踏まえて[a][b]に入る数値を考えます。
[a]は From=1、To=3 および From=3、To=1 の組合せで、Via=1 の段階で999になっています。Via=2 のループでは、経由駅 2 を介した2つの駅の距離である Dist[1][2] と Dist[2][3] の合計で更新されることになります。Via=1 ループ終了時点で、Dist[1][2]=18、Dist[2][3]=17 ですから、Dist[1][3] は「18+17=35」で更新されます(対となる Dist[3][1] についても同様です)。


b=ア:33
〔cdについて〕
O(オーダー)記法は、実行時に処理するデータ量によってアルゴリズムの計算量やメモリ使用量がどの程度増加するか、という視点でアルゴリズムを評価するものです。[c]は時間計算量、[d]は空間計算量について問うています。
- 時間計算量
- 処理を達成するために必要な時間
- 空間計算量
- 処理を達成するために必要な記憶領域の大きさ
副プログラム CalcDist は3重ループになっていて、点線で囲まれた部分はN3回、ループに入る前の print は1回、一番外側のViaループの終了時の print はN回実行されます。

次に[d]のメモリ使用量について考えます。
必要とする記憶領域の大きさは、プログラム内で使用する変数の数に依存します。副プログラム CalcDist では5つの変数を使用していて、それぞれが必要とする記憶領域は、int型変数1つ分の記憶領域を1とすると以下のように表せます。
- N … 1
- Dist … N×N=N2
- Via … 1
- From … 1
- To … 1
∴c=エ:O(N3)
d=ウ:O(N2)〔eについて〕
図2を見るとわかるように、Dist の値はDist[0][0]からDist[N][N]の対角線で要素が対称的になっています。これより、どちらかのみについて更新処理を行い、他方にはその値をコピーすることで計算回数を少なくすることが可能です。また、From と To が同じである要素は初期値が0で、プログラム中で更新されることはないので、これも計算から省くことができます。よって、更新処理が必要となる部分は以下の範囲です。
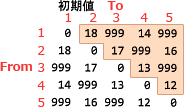
- Fromが1の場合、Toは2,3,4,5
- Fromが2の場合、Toは3,4,5
- Fromが3の場合、Toは4,5
- Fromが5の場合、Toは5
∴e=エ:From + 1, To ≦ N, 1
〔fについて〕
空欄には分岐条件式が入ります。
メモリ使用量を少なくする方法の(4)では、2駅i, j間の距離は4通りのうち最小の値になると説明されています。さらに、両駅が属する期間が同じ場合は、これに期間駅を経由せずに直接駅iから駅jに行く経路を加えて5通りのうち最小の値になるとしています。プログラムを見ると、分岐条件が真となるときに5通りの中から最小値を選択しているので、[f]には駅iと駅jが属する期間が同じ場合に真となる式が入ると判断できます。(3)の説明および表1より、その駅が属する区間の区間名は Sec に格納されているとわかるので、[f]は「Sec[i]=Sec[j]」が適切です。
なお、両端の駅が同じときに真となる「ア」も同じ区間に属していることを判定できそうですが、図4の区間Bと区間Cのように異なる区間であっても両端の駅番号が同じになる場合があるので不適切です。
∴f=ウ:Sec[i]=Sec[j]
〔gについて〕
改善後の方法では、K×Kの2次元配列 Dist に加えて、表1に示すデータを保持する記憶領域が必要となります。問題文の最後に「表1に示す表は,1駅について配列 Dist の要素5個分のメモリを使用するものとする」とあるので、駅数が N であるときの表1のサイズは 5×N になるとわかります。したがって、改善後の方法におけるメモリ使用量は「K×K+5N」の式で表せます。
一方、改善前の方法におけるメモリ使用量は[d]の解説のとおり「N2+5」です。ただし、「+5」の部分は改善後の方法でも共通なので比較する式は「N2」となります。
設問では K=5 のとき、改善後の方法におけるメモリ使用量が改善前より小さくなる N を求めたいので、2つの式の関係を不等式で表します。
5×5+5×N<N2
5N+25<N2
この式の N に解答群の数値を当てはめると、9と14のときに成り立つことがわかります。文脈的に条件を満たす最小の値を答えば良いので、[g]には「9」が入ると判断できます。
∴g=ウ:9
なお、不等式を最後まで解くと N>(5+55)/2 となります。5≒2.23なので、
(5+5×2.23)/2
=2.5+2.5×2.23
=2.5+5.575
=8.075
Nは整数ですから、計算上でも N≧9 となります。
広告
広告