平成24年春期試験午後問題　問1

午前試験免除制度対応！基本情報技術者試験のeラーニング【独習ゼミ】

問1　ハードウェア

浮動小数点数に関する次の記述を読んで，設問1，2に答えよ。
  • α×2βの形で表記される浮動小数点数を，図1に示す32ビット単精度浮動小数点形式(以下，単精度表現という)で表現する。ここで，αとβは次の条件を満たすものとする。
    　　　α＝0，又は1≦lαl＜2
    　　　－126≦β≦127
    pm01_1.png
    1. 符号部(ビット番号31)
      αの値が正のとき0，負のとき1が入る。
    2. 指数部(ビット番号30～23)
      βの値に127を加えた値が2進数で入る。
    3. 仮数部(ビット番号22～0)
      　lαlの整数部分1を省略し，残りの小数部分が，ビット番号22に小数第1位が来るような2進数で入る。
    　ただし，αの値が0の場合，符号部，指数部，仮数部ともに0とする。
  • 例えば，10進数の0.75を2進数で表すと，(0.11)2となる。これは(1.1)2×2-1と表記でき，単精度表現では，図2のとおり，符号部は(0)2，指数部は－1に127を加えて(01111110)2となり，仮数部は(1.1)2の小数部分が入るので，(100…0)2となる。ここで，00…0は0が連続していることを表す。
    pm01_2.png
広告

設問1

次の単精度表現が表す数値として正しい答えを，解答群の中から選べ。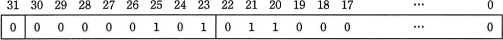
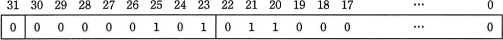
pm01_3.png
解答群
  • 3×2-125
  • 3×2-122
  • 3×25
  • 3×2132
  • 11×2-125
  • 11×2-122
  • 11×25
  • 11×2132
解答選択欄
  • 　
  • 　オ

解説

[符号部]
ビットは0なので正の値です。

[指数部]
ビット列は 00000101 は10進数表記では 5 になります。指数部の値はβに127を加えたものなので、

　β=5－127＝－122

[仮数部]
ビット列が 01100…00 は、|α|の整数部分である1が省略された小数部分だけの値なので、

　α＝1＋(0.011)2＝(1.011)2

よって設問の単精度表現は、(1.011)2×2-122 を示します。

選択肢では仮数部が3または11の整数で表現しているため、(1.011)2×2-122を仮数部が整数になるように変換すると、

　(1.011)2×2-122＝(1011)2×2-125

となります。2進数 1011 は10進数では11を指すため、仮数部を10進表記にした「11×2-125」が正解です。

∴オ：11×2-125
広告

設問2

次の記述中の　に入れる正しい答えを，解答群の中から選べ。

　二つの浮動小数点数AとBの減算と乗算を行う。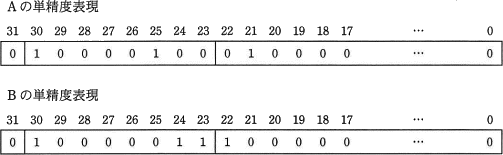
pm01_4.png
  • 減算 A－B を，次の手順①～③で行う。
    1. 指数部の値を大きい方に合わせる。Aが(1.01)2×25であることから，Bを(a)2×25とする。
    2. 減算を行う。
      　((1.01)2－(a)2)×25＝(1.0)2×2b
    3. ②の結果を単精度表現する。その結果はcとなる。
  • 乗算 A×B の結果は(d)2×29となる。
a に関する解答群
  • 0.011
  • 0.101
  • 0.11
  • 1.01
  • 1.1
b に関する解答群
  • 3
  • 4
  • 5
  • 6
  • 131
  • 132
c に関する解答群
  • pm01_5a.png
  • pm01_5i.png
  • pm01_5u.png
  • pm01_5e.png
  • pm01_5o.png
  • pm01_5ka.png
  • pm01_5ki.png
d に関する解答群
  • 1.0
  • 1.11
  • 1.1101
  • 1.111
  • 1.1111
解答選択欄
  • a:
  • b:
  • c:
  • d:
  • a=ウ
  • b=イ
  • c=イ
  • d=エ

解説

〔aについて〕
まずBが表す値を考えます。

[符号部]
符号ビットは0なので正の値です。

[指数部]
ビット列は 10000011 は10進数表記では 131 になります。指数部の値はβに127を加えたものなので、

　β=131－127＝4

[仮数部]
ビット列が 100…00 は、|α|の整数部分である1が省略された小数部分だけの値なので、

　α＝1＋(0.1)2＝(1.1)2

よってBは、(1.1)2×24 を示します。

①の手順では指数部の値を大きい方に合わせます。Aの指数部が 5 なので、Bを指数部が 5 になるように変換します。

　(1.1)2×24＝(0.11)2×25

∴a＝ウ：0.11

〔bについて〕
A－Bは以下の手順で演算を行います。

　(1.01)2×25－(0.11)2×25
＝((1.01)2－(0.11)2)×25
＝(0.1)2×25
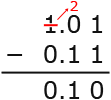
pm01_6.png
さらにbが指数部となっている値の仮数部は(1.0)2になっているため、(0.1)2×25の仮数部が(1.0)2になるように変換します。

　(0.1)2×25＝(1.0)2×24

∴b＝イ：4

〔cについて〕
②の結果は上記で計算した「(1.0)2×24」です。

[符号部]
正の値なので符号ビットは0になります。

[指数部]
βの値4に127を加えた131を2進数表記にした 10000011 が入ります。

[仮数部]
仮数部には |α|の値 (1.0)2 の小数部分が格納されます。小数部分は 0 なので、仮数部のビット列は 00…00になります。

上記3つのビット列をつなぎ合わせると「イ」の単精度表現になります。
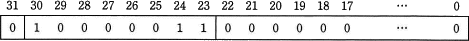
pm01_5i.png
∴c＝イ

〔dについて〕
2進数同士の乗算は10進数の乗算を筆算で行うのと同じ要領で行うことができます。

　(1.01)2×25×(1.1)2×24
＝((1.01)2×(1.1)2)×29
＝(1.111)2×29
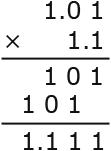
pm01_7.png
また"(1.01)2×(1.1)2"の部分は、一旦10進数に変換してから乗算を行い、再び2進数に戻す方法でも計算可能です。

　(1.01)2×(1.1)2
＝1.25×1.5＝1.875
＝1＋0.5＋0.25＋0.125
＝1＋2-1＋2-2＋2-3
＝(1.111)2

∴d＝エ：1.111
広告
広告

次の問題

▲
Pagetop