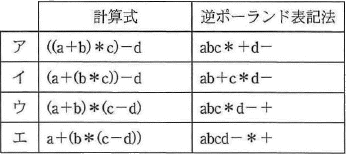
平成26年秋期試験問題 午前問4

広告
解説
逆ポーランド表記法(後置表記法)は、演算子を2つの被演算子の右側に記述する表記法です。通常の数式の「A+B」を逆ポーランド表記法で表現すると「AB+」となります。
通常の式を逆ポーランド表記法で表現するときには、通常の式を計算するとの同じ順番(括弧の中優先、剰余算優先)で、普通に計算式を解くのと同じ要領で変換していきます。一度変換した部分はひとまとまりの項として扱うことがポイントです。
以下の式では、変換対象をわかりやすくするために変換対象となる左項を青、右項を赤で示しています。
通常の式を逆ポーランド表記法で表現するときには、通常の式を計算するとの同じ順番(括弧の中優先、剰余算優先)で、普通に計算式を解くのと同じ要領で変換していきます。一度変換した部分はひとまとまりの項として扱うことがポイントです。
以下の式では、変換対象をわかりやすくするために変換対象となる左項を青、右項を赤で示しています。
- ((a+b)*c)-d
→(ab+*c)-d
→ab+c*-d
→ab+c*d-
異なるため誤りです。 - (a+(b*c))-d
→(a+bc*)-d
→abc*+-d
→abc*+d-
異なるため誤りです。 - (a+b)*(c-d)
→ab+*cd-
→ab+cd-*
異なるため誤りです。 - a+(b*(c-d))
→a+(b*cd-)
→a+bcd-*
→abcd-*+
変換結果が設問の表の式と一致するため適切な組合せです。
広告