平成26年春期試験午後問題　問8

午前試験免除制度対応！基本情報技術者試験のeラーニング【独習ゼミ】

問8　データ構造及びアルゴリズム

次のアルゴリズムの説明を読んで，設問1～3に答えよ。

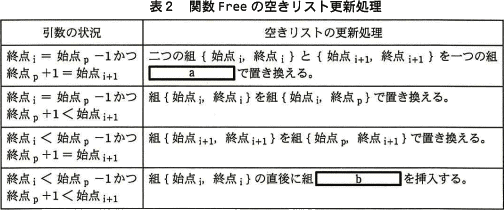
　セルを1列に連続して並べた領域がある。この領域中のセルについて，割当てと解放の処理を行う。
　各セルには，セル位置を指定するための連続する整数が対応している。領域のセル数や，対応する整数の範囲には，特に制限がない。
　各セルは，"空き"又は"割当済み"のいずれかの状態にある。現在，領域中のどのセルが"空き"の状態にあるかという情報を，空きリストとして保持している。
　関数 Alloc(始点，終点) は，引数で指定した始点から終点までの連続した"空き"セルを"割当済み"として，空きリストから取り除く。関数 Free(始点，終点) は，引数で指定した始点から終点までの連続した"割当済み"セルを"空き"として，空きリストに戻す。

[空きリストの説明〕
　空きリストの形式を，次に示す。

　　{{始点1，終点1}，{始点2，終点2}，…，{始点N，終点N}}

{始点i，終点i}(始点i≦終点i)は，一つの連続した"空き"セルの先頭位置と終端位置の組(以下，組という)で，始点1＜始点2＜…＜始点Nである。
　割当て・解放の処理と空きリストの状態の例を，次の(1)～(3)に示す。ここで，セル　中の数字は，セル位置を表す。また，　は"空き"を，　は"割当済み"を，それぞれ表す。
  • 領域の初期状態は，全セルが空いている。空きリストは{{-∞，+∞}}で表す。
    pm08_1.png
    　ここで，記号"-∞"は，領域中のどのセル位置の値よりも小さい整数を表し，記号"+∞"は，領域中のどのセル位置の値よりも大きい整数を表すものとする。また，セル位置-∞～+∞のうち，領域外の部分には"空き"セルが並んでいるものとする。
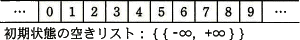
  • 関数 Alloc で"割当済み"としたセルは，空きリストから取り除く。例えば，(1)の初期状態から，Alloc(1，2) と Alloc(6，8) を実行すると，次のようになる。
    pm08_2.png
    　実行後，空きリスト中の組の個数は 3 となる。
  • 関数 Free で解放したセルは，空きリストに戻す。例えば，(2)の実行後の状態から，Free(6，7) を実行すると，次のようになる。
    pm08_3.png
    　実行後，解放された"空き"セルの組{6，7}は，実行前の"空き"セルの組{3，5}とつながって一つの連続した"空き"セルの組{3，7}となるので，空きリスト中の組の個数は 3 となる。
〔関数 Alloc の説明〕
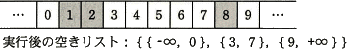
　関数 Alloc(始点P，終点P) の処理手順は，次のとおりである。
　なお，引数の値は，-∞＜始点P≦終点P＜+∞を満たしているものとする。
  • 空きリスト中に，始点i≦始点Pかつ終点P≦終点iを満たす組｛始点i，終点i｝が存在すれば(2)へ進む。存在しなければ，"一部又は全体が割当済み"を表示して，処理を終了する。
  • 割当てが可能であるので，表1に従って，引数の状況に対応した空きリストの更新処理を実行して，処理を終了する。
pm08_4.png
〔関数 Free の説明〕
　関数 Free(始点P，終点P) の処理手順は，次のとおりである。
　なお，引数の値は，-∞＜始点P≦終点P＜+∞を満たしているものとする。
  • 空きリスト中に，終点i＜始点Pかつ終点P＜始点i+1を満たす連続する二つの組{始点i，終点i}と{始点i+1，終点i+1}が存在すれば(2)へ進む。存在しなければ，"一部又は全体が割当済みでない"を表示して，処理を終了する。
  • 解放が可能であるので，表2に従って，引数の状況に対応した空きリストの更新処理を実行して，処理を終了する。
pm08_5.png
広告

設問1

本文中の　に入れる正しい答えを，解答群の中から選べ。
a，b に関する解答群
  • {始点i，終点i+1}
  • {始点i，終点p}
  • {始点p，終点i+1}
  • {始点p，終点p}
解答選択欄
  • a:
  • b:
  • a=ア
  • b=エ

解説

関数 Free の空きリストの更新処理は、引数の状況によって下記の4パターンに分かれます。ここでpが付いているのは引数、iが付いているのは空きリスト中の任意の要素を表しています。
1. 終点i=始点p-1 かつ 終点p+1=始点i+1の場合
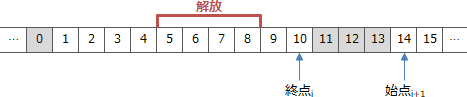
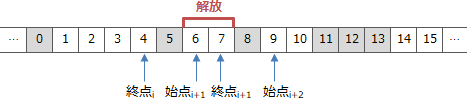
解放開始位置の1つ前がi番目の要素の終点、解放終了位置の1つ後がi+1番目の要素の始点、すなわち、ある空き領域の直後から、次の空き領域の直前までが解放対象となるときです。例えば次のような状況です。
  • 実行後の空きリストのi番目が{1,4}
  • 実行後の空きリストのi+1番目が{9,10}
  • 関数Freeの引数が5と8
pm08_7.png
この場合、空きリストの更新処理を実施すると以下のように前後の空き領域が1つにまとまります。更新内容としては、i番目の要素の終点を10に変更し、i+1番目の要素{9,10}を削除することになります。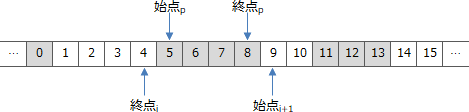
pm08_8.png
2. 終点i=始点p-1 かつ 終点p+1＜始点i+1の場合
解放開始位置の1つ前がi番目の要素の終点で、解放終了位置の1つ後がi+1番目の要素の始点よりも小さい、すなわち、ある空き領域の直後から、割当て済領域の途中までが解放対象となる場合です。例えば次のような状況です。
  • 実行後の空きリストのi番目が{1,4}
  • 行後の空きリストのi+1番目が{9,10}
  • 関数Freeの引数が5と7
pm08_9.png
この場合、空きリストの更新処理を実施すると以下のようにi番目の要素の終点が解放終了位置まで後ろに伸びます。更新内容としては、i番目の要素の終点を7に変更することになります。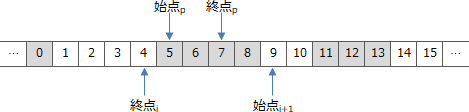
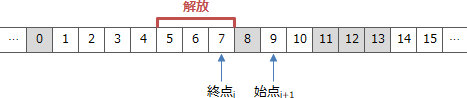
pm08_10.png
3. 終点i＜始点p-1 かつ 終点p+1=始点i+1の場合
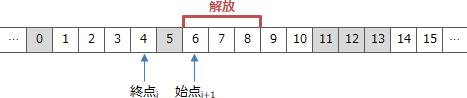
解放開始位置の1つ前がi番目の要素の終点より大きく、解放終了位置の1つ後がi+1番目の要素の始点、すなわち、割当て済領域の途中から、次の空き領域の直前までが解放対象となる場合です。例えば次のような状況です。
  • 実行後の空きリストのi番目が{1,4}
  • 実行後の空きリストのi+1番目が{9,10}
  • 関数Freeの引数が6と8
pm08_11.png
この場合、空きリストの更新処理を実施すると以下のようにi+1番目の要素の始点が解放開始位置まで前に伸びます。更新内容としては、i+1番目の要素の始点を6に変更することになります。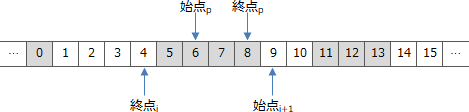
pm08_12.png
4. 終点i＜始点p-1 かつ 終点p+1＜始点i+1の場合
解放開始位置の1つ前がi番目の要素の終点より大きく、解放終了位置の1つ後がi+1番目の要素の始点より小さい、すなわち、割当て済領域の途中から途中までが解放対象となる場合です。例えば次のような状況です。
  • 実行後の空きリストのi番目が{1,4}
  • 実行後の空きリストのi+1番目が{9,10}
  • 関数Freeの引数が6と7
pm08_13.png
この場合、空きリストの更新処理を実施すると、以下のように引数の始点と終点をもつ新たな空き領域が生まれます。更新内容としては、i番目の要素の直後に要素{6,7}を挿入することになります。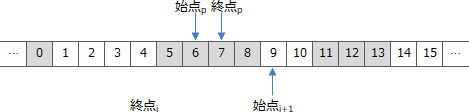
pm08_14.png
〔aについて〕
パターン1に該当するので、置き換える要素は元の2つの要素の範囲をつなげた{始点i, 終点i+1}となります。

∴a＝ア：{始点i, 終点i+1}

〔bについて〕
パターン4に該当するので、挿入する要素は引数の2点を値として持つ{始点p, 終点p}となります。

∴b＝エ：{始点p, 終点p}
広告

設問2

次のプログラム中の　に入れる正しい答えを，解答群の中から選べ。

　関数 Alloc の説明に基づいて，プログラムを作成した。
　空きリスト中の現在の組の個数は大域整数型変数 N に格納されている。空きリスト{{始点1，終点1}，{始点2，終点2}，…，{始点N，終点N}}については，始点i(i：1，2，…，N)の値は大域整数型配列始点の要素 始点[i] に，終点i(i：1，2，…，N)の値は大域整数型配列 終点 の要素 終点[i] に，それぞれ格納されている。これらの配列は，十分に大きいものとする。
pm08_6.png
c，d に関する解答群
  • 始点[I] ← 始点P－1
  • 始点[I] ← 終点P＋1
  • 終点[I] ← 始点P－1
  • 終点[I] ← 終点P＋1
e に関する解答群
  • I＋1，L ＜ N，1
  • I＋1，L ≦ N，1
  • N，L ≧ I＋1，－1
  • N，L ＞ I＋1，－1
解答選択欄
  • c:
  • d:
  • e:
  • c=イ
  • d=ウ
  • e=ウ

解説

関数 Alloc の割当て処理は、引数の状況によって下記の4パターンに分かれます。
1. 始点i=始点p かつ 終点p=終点iの場合
見つかった空き領域と割り当てる領域のサイズが同一の場合です。この場合、空きリストの当該要素を削除します。プログラム中では一つずつ前にシフトさせることで削除しています。
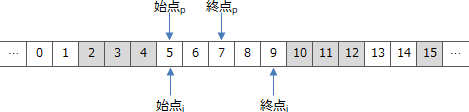
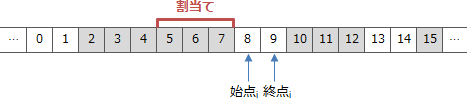
2. 始点i=始点p かつ 終点p＜終点iの場合
ある空き領域の始点から途中までを割当てする場合です。例えば次のような状況です。
pm08_15.png
この場合、空きリストの更新処理を実施すると以下のように空き領域の始点が割当て対象領域の1つ後までずれます。更新内容としては、i番目の要素の始点を8に変更することになります。
pm08_16.png
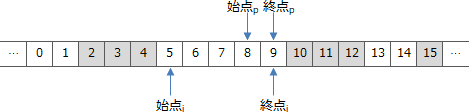
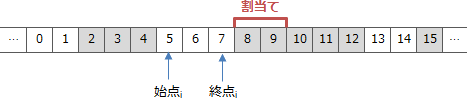
3. 始点i＜始点p かつ 終点p=終点iの場合
ある空き領域の途中から終点までを割当てする場合です。例えば次のような状況です。
pm08_17.png
この場合、空きリストの更新処理を実施すると以下のように空き領域の終点が割当て対象領域の1つ前までずれます。更新内容としては、i番目の要素の終点を7に変更することになります。
pm08_18.png
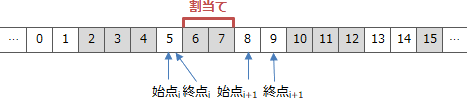
4. 始点i＜始点p かつ 終点p＜終点iの場合
ある空き領域の途中から途中までを割当てする場合です。例えば次のような状況です。
pm08_19.png
この場合、空きリストの更新処理を実施すると以下のように空き領域が2つに分かれます。更新内容としては、i番目の要素の終点を5に変更し、空きリストに新たな要素として{8,9}を挿入することになります。
pm08_20.png
〔cについて〕
パターン2の処理に該当します。行うべき処理は、i番目の要素の始点を終点Pの1つ後に設定することなので「始点[I] ← 終点P＋1」が適切です。

∴c＝イ：始点[I] ← 終点P＋1

〔dについて〕
パターン3の処理に該当します。行うべき処理は、i番目の要素の終点を始点Pの1つ前に設定することなので「終点[I] ← 始点P－1」が適切です。

∴d＝ウ：終点[I] ← 始点P－1

〔eについて〕
パターン4の処理に該当します。[e]を含むループ処理の直後にはパターン4の所で説明した、i番目の要素の終点の更新、始点を終点P+1、終点を終点Iとする要素の追加を行っています。新たな要素が設定されるのはi+1番目の要素であるため、この設定処理の前に元のi+1番目以降にある要素を1つずつ後ろにずらしておく必要があります。これを行うのが[e]を含むループ処理です。

ループの処理を見ると、L番目の要素をL+1番目に移動することを繰り返しています。後ろにシフトさせる操作では後ろの要素から順に行わないと後方の要素を上書きすることになってしまうので、現在の空きリストの個数が格納されている大域変数 N を使って、NからI+1まで1ずつ減らしながら繰り返す条件式が適切です。こうすることで、N番目の要素はN+1番目に、N-1番目の要素はN番目に…、I+1番目の要素はI+2番目に移動することになります。

「ア」「イ」は前の要素から順にシフトさせているので誤り、「エ」はI+1番目の要素の移動が行われないので誤りです。

∴e＝ウ：N，L ≧ I＋1，－1
広告

設問3

次の記述中の　に入れる適切な答えを，解答群の中から選べ。

　このアルゴリズムでは，空きリスト{{始点1，終点1}，{始点2，終点2}，…，{始点N，終点N}}の始点1に値 -∞ を，終点Nに値 +∞ をそれぞれ設定している。このような設定をすることの利点の一つに，fという特徴が挙げられる。
　また，このアルゴリズムでは，空きリスト中の組の個数が変化する。領域中のセル数が E 個であるとする。このとき，空きリスト中の組の個数は，最大でgとなる。また，E 個の全てのセルが"割当済み"となったとき，空きリスト中の組の個数は，hとなる。ここで，整数同士の除算では，商の小数点以下を切り捨てる。
f に関する解答群
  • 空きリストが空(組の個数が0)にならない
  • 関数 Free の実行時に空きリスト中の組の個数が 2 以上であることが保証される
  • 始点1 又は 終点N の値が変わらない限り領域中に"空き"セルが残っている
  • 領域中の一つの連続した"空き"セルが幾ら長くても一つの組で表せる
g，h に関する解答群
  • 1
  • 2
  • E÷2＋1
  • (E＋1)÷2＋1
  • E＋1
  • E＋2
解答選択欄
  • f:
  • g:
  • h:
  • f=ア
  • g=エ
  • h=イ

解説

〔fについて〕
  • 正しい。Alloc および Free では空き領域を基準に更新処理を行っています。もし空き領域がなくなるとプログラムが期待通りに動作しません。領域内に空きセルがなくなった場合でも、∞を使用することで空き領域の組を常に1つ以上存在させておくことができます。
  • 空きリストが組{-∞,+∞}のみの場合でも、関数Freeが実行される可能性があります。よって不適切です。この場合、"一部または全部が割当て済でない"として終了します。
  • 領域内のすべてのセルを使用すれば空きセルはなくなります。よって不適切です。
  • 空き領域を組{始点,終点}で表すことの利点であり、∞を設定することの利点ではありません。
∴f＝ア：空きリストが空(組の個数が0)にならない

〔gについて〕
空きリストの組が最大数となるのは、大きさ1の空き領域と、大きさ1の割当て済領域が連続する場合です。
例えば、セルの数が5（E=5）のときは、以下のような空きリストの組が最大となります。※領域外のセルは割当てはできませんが空きセルが並んでいるので位置としては参照可能です。
pm08_21.png
このときの空きリストの組の個数は4です。またセルの数が6（E=6）のときは、以下のような空きリストの組が最大なります。
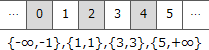
pm08_22.png
E=5と場合と同じで組の個数は4です。

選択肢の中で、E=5のとき4、E=6のとき4となる式は「エ」だけです。

∴g＝エ：(E＋1)÷2＋1

〔hについて〕
例えばセルの数が5（E=5）のとき、空き領域がなくなると空きリストの組は以下の2つになります。
pm08_23.png
この場合、領域内のセルの数の多寡にかかわらず空きリストの組の個数は2となります。

∴g＝イ：2
広告
広告

前の問題次の問題

▲
Pagetop