平成27年秋期試験問題 午前問23
問23解説へ
図のNANDゲートの組合せ回路で，入力A，B，C，Dに対する出力Xの論理式はどれか。ここで，論理式中の"・"は論理積，"＋"は論理和を表す。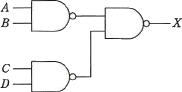
- (A＋B)・(C＋D)
- A＋B＋C＋D
- A・B＋C・D
- A・B・C・D
広告
解説
NAND回路のNANDは"NOT AND"を表していて、AND回路の出力を反転させた回路です。したがって、二つの入力が共に1の時だけ0を出力し、その他の場合は1を出力します。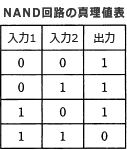
論理回路から導いた論理式を変形する方法と、ベン図を使用する方法の2通りでの解法を説明します。
[論理式を使う方法]
NAND回路を論理式で表すと「A・B」となるため、設問の組合せ回路は、
A・B・C・D
と表すことができます。これをド・モルガン則を利用して変形すると、
A・B・C・D
＝A・B＋C・D //A・B＝A＋Bを適用
＝A・B＋C・D //A＝Aを適用
[ベン図を使う方法]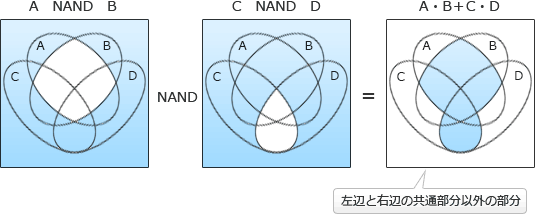
[論理式を使う方法]
NAND回路を論理式で表すと「A・B」となるため、設問の組合せ回路は、
A・B・C・D
と表すことができます。これをド・モルガン則を利用して変形すると、
A・B・C・D
＝A・B＋C・D //A・B＝A＋Bを適用
＝A・B＋C・D //A＝Aを適用
[ベン図を使う方法]
広告