平成27年春期試験問題 午前問23

問23解説へ
図に示すデジタル回路と等価な論理式はどれか。ここで,論理式中の・は論理積,+は論理和,XはXの否定を表す。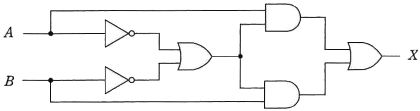

- X=A・B+A・B
- X=A・B+A・B
- X=A・B+A・B
- X=(A+B)・(A+B)
広告
解説
複雑な論理回路図の問題では、手間はかかりますが確実に答えがでる方法で解くのがおすすめです。
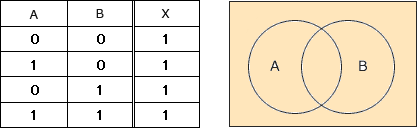
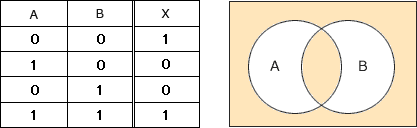
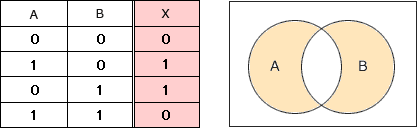
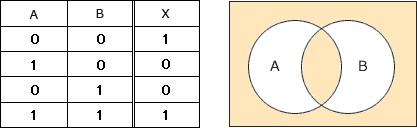
まず(A=0, B=0),(A=1, B=0),(A=0, B=1),(A=1, B=1)の4つのケースについて回路図を追跡し、結果Xを真理値表にまとめます。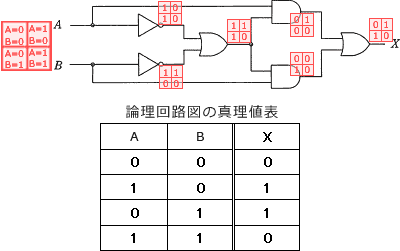 設問の論理回路図は「XOR回路」と等価であることがわかります。
設問の論理回路図は「XOR回路」と等価であることがわかります。
次に各選択肢の論理式を解いて、回路図と一致するものを探します。
またこの設問を早く解く方法として、回路図を論理式で表した後、それを変形する方法があります。(掲示板No.0272のスレッドより)
回路図より、
X =A・(A+B) + (A+B)・B
=A・A + A・B + A・B + B・B //分配の法則を適用
=0 + A・B + A・B + 0 //A・A=0を適用
=A・B + A・B //0+A=Aを適用
上記の論理式は「ウ」と一致するため正解とわかります。
まず(A=0, B=0),(A=1, B=0),(A=0, B=1),(A=1, B=1)の4つのケースについて回路図を追跡し、結果Xを真理値表にまとめます。

次に各選択肢の論理式を解いて、回路図と一致するものを探します。
またこの設問を早く解く方法として、回路図を論理式で表した後、それを変形する方法があります。(掲示板No.0272のスレッドより)
回路図より、
X =A・(A+B) + (A+B)・B
=A・A + A・B + A・B + B・B //分配の法則を適用
=0 + A・B + A・B + 0 //A・A=0を適用
=A・B + A・B //0+A=Aを適用
上記の論理式は「ウ」と一致するため正解とわかります。
広告