平成28年春期試験午後問題　問9

午前試験免除制度対応！基本情報技術者試験のeラーニング【独習ゼミ】

問9　ソフトウェア開発(C)

次のCプログラムの説明及びプログラムを読んで，設問1～3に答えよ。

〔プログラムの説明〕
　図形の一部を拡大すると，再び同じパターンの図形が現れる自己相似性をもつ図形を，フラクタル図形と呼ぶ。関数 print_frac は，文字"＊"及び空白文字を二次元の格子状に並べてフラクタル図形を描画するプログラムである。
  • 関数 print_frac が描画するフラクタル図形の例を，図1に示す。
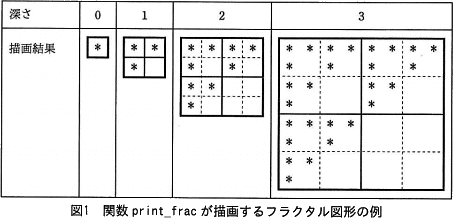
    pm09_1.png
    1. 深さが0の図形は，1行1列の文字"＊"から成る図形である。
    2. 深さが1以上の図形は，深さが0の図形に対して，(2)で説明する生成規則を，深さの回数だけ繰返し適用して得られる図形である。
  • 深さが d(1以上) の図形は，深さが d－1 の図形を構成する一つ一つの文字を，文字"＊"であるか空白文字であるかに応じて，図2に示す生成規則のとおりに，文字の行列で置換したものである。
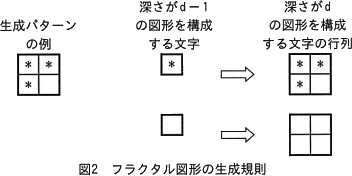
    pm09_2.png
    1. 文字"＊"の部分は，生成パターンと呼ぶ文字の行列で置換する。
    2. 空白文字の部分は，生成パターンと同じ大きさで全ての要素が空白文字の行列で置換する。
  • 生成パターンは，二次元の配列変数 pat によって与える。pat の各要素の値は，空白文字を表す0，又は文字"＊"を表す1である。pat の行数，列数及び内容を変更することで，異なるフラクタル図形を描画することができる。
  • 関数 print_frac の仕様は次のとおりである。
    機能:
    深さがdのフラクタル図形を描画する。
    引数:
    d　フラクタル図形の深さ
  • 関数 print_frac で使用している関数 exists_at の仕様は次のとおりである。
    機能:
    深さがdのフラクタル図形のi行j列目が空白文字であるか文字"＊"であるかを判定する。
    引数:
    i　行数(一番上の行を0行目とする)
    j　列数(一番左の列を0列目とする)
    d　フラクタル図形の深さ
    返却値:
    判定結果(0: 空白文字，1: 文字"＊")
　ここで，関数の引数に誤りはないものとする。
pm09_3.png
広告

設問1

深さが2の図形と深さが3の図形は次のとおりである。深さが3の図形において，深さが2の図形の斜線部を置換した部分として正しい答えを，解答群の中から選べ。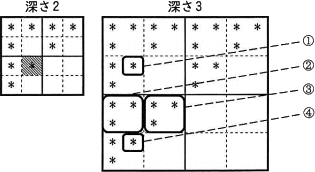
pm09_4.png
解答群
  • ①
  • ②
  • ③
  • ④
解答選択欄
  • 　
  • 　ウ

解説

〔プログラムの説明〕(2)の説明にあるように、深さ2のフラクタル図形を深さ3に変換した場合、深さ2の1マスは深さ3の2×2マスに対応します。網掛け位置の文字は"*"ですので、pm09_6.pngに変換されているはずです。位置関係を比較すると次のエリア同士が対応していることがわかります。
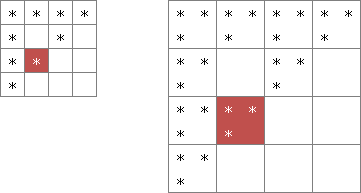
pm09_7.png
∴ウ：③
広告

設問2

配列変数 pat を変更して，深さが3の図形を描画したところ，次のとおりになった。配列変数 pat の変更内容として正しい答えを，解答群の中から選べ。
pm09_5.png
解答群
  • int pat[2][3]＝{
    　{0，1，0},
    　{1，0，1}
    };
  • int pat[2][3]＝{
    　{1，1，1},
    　{1，0，1}
    };
  • int pat[2][3]＝{
    　{0，1，0},
    　{1，1，1},
    　{1，0，1}
    };
  • int pat[2][3]＝{
    　{1，1，1},
    　{1，0，1},
    　{1，0，1}
    };
解答選択欄
  • 　
  • 　イ

解説

設問1では、生成パターン（以後、配列変数 pat ）は2×2のパターンが使用されています。そのため、深さ d が1増える毎に1マスが2×2のマスに変化します。このパターンを使うと、深さ d が1増える毎にフラクタル図形の行数は以下のように変化します（列数も同様）。　

　1、2、4、8、16、32、…

これより、配列変数patの行数、深さd、フラクタル図形の行数・列数は以下のような関係にあることがわかります。

　(フラクタル図形の行数) = (配列変数patの行数)の(深さd)乗
　(フラクタル図形の列数) = (配列変数patの列数)の(深さd)乗

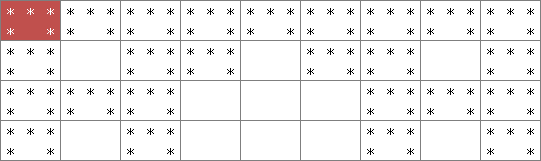
設問2の図形を見てみると、深さが3で8×27の図形となっているので以下の式が成り立ちます。

　8 = 23
　27 = 33

よって、配列変数 pat は2×3の配列であることがわかります。

設問2の図を2×3の図形に分割すると以下のようになります。
pm09_8.png
したがって正しい生成パターンは「イ」です。
広告

設問3

プログラム中の　に入れる正しい答えを，解答群の中から選べ。
a に関する解答群
  • p_rn += rn;
    p_cn += cn;
  • p_rn *= rn;
    p_cn *= cn;
  • rn += p_rn;
    cn += p_cn;
  • rn *= p_rn;
    cn *= p_cn;
b，c，d に関する解答群
  • 0
  • 1
  • pat[i][j]
  • pat[i % d][j % d]
  • pat[i / d][j / d]
  • pat[i % p_rn][j % p_cn]
  • pat[i / p_rn][j / p_cn]
解答選択欄
  • a:
  • b:
  • c:
  • d:
  • a=エ
  • b=イ
  • c=ア
  • d=カ

解説

〔aについて〕
変数 p_rn と変数 p_cn はプログラム中の初期化処理より、以下を表現していることがわかります。
  • p_rn：配列変数 pat の行数（p_rn…pattern row num）
  • p_cn：配列変数 pat の列数（p_cn…pattern col num）
また、変数 rn と変数 cn は関数 print_frac 内の使用方法より、以下を表現していることがわかります。
  • rn：関数 print_frac で出力するフラクタル図形の行数
  • cn：関数 print_frac で出力するフラクタル図形の列数
しかし、変数 rn と変数 cn は1を代入したあと、処理がされていません。for文の二重ループでは繰返し回数の上限として rn と cn を使用しているので、[a]にはフラクタル図形の行数と列数を rn と cn に代入する処理が入ると判断できます。この時点で、p_rn、p_cn に代入している「ア」「イ」は正解の候補から除外することができます。

設問2より、フラクタル図形の行数と列数は以下のように決定されます。

　(フラクタル図形の行数) = (配列変数patの行数)の(深さd)乗
　(フラクタル図形の列数) = (配列変数patの列数)の(深さd)乗

パターンが2×3、深さが d のとき適切な行と列の数は、
  • d=0 のとき 1行1列
  • d=1 のとき 2行3列
  • d=2 のとき 4行9列
  • d=3 のとき 8行27列
ですので、初期値の1に対して生成パターンの行数、列数を d 回だけ乗じれば正しい大きさを得られることになります。したがって「エ」が正解となります。

∴a＝エ：rn *= p_rn; cn *= p_cn;

〔bについて〕
関数 exists_at が0を返したときは空白となり、1を返したときには"*"が描画されます。〔プログラムの説明〕(1)の①に「深さが0の図形は，1行1列の文字"＊"から成る図形である」とあります。引数 d はフラクタル図形の深さを表す変数ですので、d == 0（つまり深さ0）の場合は関数 exists_at は必ず1を返す必要があります。

∴b＝イ：1

〔cについて〕
関数 exists_at が0を返したときに行う処理です。

まず、引数の i/p_rn と j/p_cn について説明します。
設問1より、深さ2と深さ3のフラクタル図形間の置換関係は以下のようになっていることがわかります。
pm09_9.png
これより、深さ3の要素位置を深さ2の要素位置に変換する場合、配列変数 pat の行（または列数）で割ったときの商を求める必要があります。C言語の場合、int型は切り捨てで計算がされるため、i/p_rn と j/p_cn で商を求めることができます。i/p_rn と j/p_cn を関数 exists_at の引数に与えることで、深さ d が変化した場合の要素の整合性をとっています。

〔プログラムの説明〕(2)より、深さが d-1 の図形を構成する文字が0（空白）の場合（すなわち、関数 exists_at の戻り値が0の場合）、深さ d の図形要素はすべて0（空白）になります。これより「ア」が正解となります。

∴c＝ア：0

〔dについて〕
深さ d-1 のフラクタル図形を構成する文字が"*"だったときの処理が入ります。図1の深さ2の図形を例にすると、行 i 列 j と、生成パターン中の出力する文字は以下のように対応しています。
pm09_10.png
関数 exists_at の引数である i と j から適切な pat の添え字を求めるには、i を p_rn で割った余りを pat の行位置とし、j を p_cn で割った余りを pat の列位置とすれば良いことがわかります。C言語で除算の余りを求めるには「%」演算子を使います。したがってdには「カ」が入ります。

∴d＝カ：pat[i % p_rn][j % p_cn]
広告
広告

前の問題次の問題

▲
Pagetop