平成29年秋期試験午後問題　問8

午前試験免除制度対応！基本情報技術者試験のeラーニング【独習ゼミ】

問8　データ構造及びアルゴリズム

次のプログラムの説明及びプログラムを読んで，設問1～4に答えよ。

　文字列の誤りを検出するために，N種類の文字に0，1，…，N－1の整数値を重複なく割り当て，検査文字を生成するプログラムと，元となる文字列の末尾に検査文字を追加した検査文字付文字列を検証するプログラムである。ここで扱う30種類の文字，及び文字に割り当てた数値を，表1に示す。空白文字は"␣"と表記する。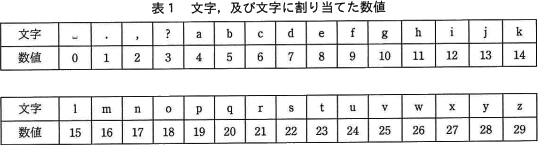
pm08_1.png
〔プログラムの説明〕
　検査文字の生成と検査文字付文字列の検証の手順を示す。
(1) 検査文字の生成
  1. 文字列の末尾の文字を1番目の文字とし，文字列の先頭に向かって奇数番目の文字に割り当てた数値を2倍してNで割り，商と余りの和を求め，全て足し合わせる。
  2. 偶数番目の文字に割り当てた数値は，そのまま全て足し合わせる。
  3. ①と②の結果を足し合わせる。
  4. Nから，③で求めた総和をNで割った余りを引く。さらにその結果を，Nで割り，余りを求める。求めた数値に対応する文字を検査文字とする。
(2) 検査文字付文字列の検証
  1. 検査文字付文字列の末尾の文字を1番目の文字とし，文字列の先頭に向かって偶数番目の文字に割り当てた数値を2倍してNで割り，商と余りの和を求め，全て足し合わせる。
  2. 奇数番目の文字に割り当てた数値は，そのまま全て足し合わせる。
  3. ①と②の結果を足し合わせる。
  4. ③で求めた総和がNで割り切れる場合は，検査文字付文字列に誤りがないと判定する。Nで割り切れない場合は，検査文字付文字列に誤りがあると判定する。

〔検査文字付文字列の生成例〕
　表1及び検査文字の生成の手順を用いることによって，文字列 ipa␣␣ に対し，生成される検査文字は f である。
　検査文字付文字列は，文字列の末尾に検査文字を追加し，ipa␣␣fとなる。

〔プログラムの仕様〕
　各関数の仕様を(1)～(4)に示す。ここで，配列の添字は1から始まるものとする。
  • 関数 calcCheckCharacter は，文字列及び文字列長を用いて生成した検査文字を返す。関数 calcCheckCharacter の引数及び返却値の仕様は，表2のとおりである。
    pm08_2.png
    関数 calcCheckCharacter は，関数 getValue，関数 getChar を使用する。
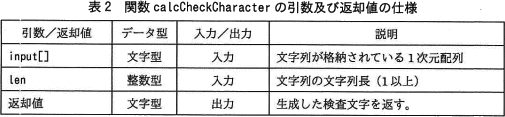
  • 関数 validateCheckCharacter は，検査文字付文字列を検証し，検証結果を返す。関数 validateCheckCharacter の引数及び返却値の仕様は，表3のとおりである。
    pm08_3.png
    　関数 validateCheckCharacter は，関数 getValue を使用する。
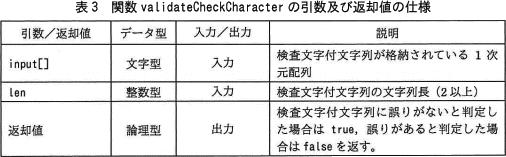
  • 関数 getValue は，表1に従い，引数として与えられた文字に割り当てた数値を返す。
  • 関数 getChar は，表1に従い，引数として与えられた数値に対応する文字を返す。
広告

設問1

プログラム中の　に入れる正しい答えを，解答群の中から選べ。ここで，a1とa2に入れる答えは，aに関する解答群の中から組合せとして正しいものを選ぶものとする。
pm08_4.png
a に関する解答群
pm08_5.png
b に関する解答群
  • N - sum % N
  • sum % N
  • (N - sum % N) % N
  • (sum % N) % N
c に関する解答群
  • sum ÷ N ＝ 0
  • sum ÷ N ≠ 0
  • sum % N ＝ 0
  • sum % N ≠ 0
解答選択欄
  • a:
  • b:
  • c:
  • a=エ
  • b=ウ
  • c=エ

解説

設問の解説に入る前に例示されている ipa␣␣ → ipa␣␣f を用いて基本となる処理過程を確認しておきます。

[検査文字の生成]
ipa␣␣ の文字のうち後ろから数えて奇数番目の文字は2倍してN(=30)で割って足します。偶数番目の文字はそのまま足します。
  • ␣ → 0×2÷30＝0 余り 0
  • ␣ → 0
  • a → 4×2÷30＝0 余り 8
  • p → 19
  • i → 12×2÷30＝0 余り 24
　総和＝0＋0＋8＋19＋24＝51

総和(=51)をNで割った余りを求め、Nから引きます。さらにその結果をNで割った余りが検査文字です。
  • 51÷30＝1 余り 21
  • 30－21＝9
  • 9÷30＝0 余り 9
  • 9 → f //検査文字はf

[検査文字付文字列の検証]
まず ipa␣␣f の文字のうち後ろから数えて偶数番目の文字は2倍してN(=30)で割って足します。奇数番目の文字はそのまま足します。
  • f →9
  • ␣ → 0×2÷30＝0 余り 0
  • ␣ → 0
  • a → 4×2÷30＝0 余り 8
  • p → 19
  • i → 12×2÷30＝0 余り 24
　総和＝9＋0＋0＋8＋19＋24＝60

総和がN(=30)で割り切れるので"誤りなし"と判定されます。

〔aについて〕
まずa1について考えます。

関数 calcCheckCharacter で使用されている is_even は論理型の変数です。is_evenの真偽により分岐する処理を見てみると、
sum ← sum + value …①
は、数値をそのままsum(総和を格納する変数)に加算しているので偶数番目の文字への処理であり、
sum ← sum + (value × 2) ÷ N + (value × 2) % N …②
は、valueの2倍をNで割った商と余りをsumに加算しているので、奇数番目の文字への処理とわかります。

総和を求める処理は文字列の末尾(len)から順に行われ、is_evenの初期値はfalseです。つまり1文字目は is_even=false の状態で分岐判定されます。後ろから1文字目(奇数番目)には②の処理を適用しなくてはならないため、これに合致するような分岐条件である必要があります。1文字目に②の処理を適用するにはa1がtrueになっている必要があります。a1にfalseが指定されていると、奇数番目の文字に対して①の処理が適用されてしまうため指示通りの処理となりません。

次にa2について考えます。

関数 validateCheckCharacter で使用されている is_odd も論理型の変数です。is_oddの真偽により分岐する処理を見てみると、
sum ← sum + value …①
は、数値をそのままsum(総和を格納する変数)に加算しているので奇数番目の文字への処理であり、
sum ← sum + (value × 2) ÷ N + (value × 2) % N …②
は、valueの2倍をNで割った商と余りをsumに加算しているので、偶数番目の文字への処理とわかります。

総和を求める処理は文字列の末尾(len)から順に行われ、is_oddの初期値はtrueです。つまり1文字目は is_odd=true の状態で分岐判定されます。先程とは逆に後ろから1文字目(奇数番目)には①の処理を適用しなくてはならないため、a2はtrueになっている必要があります。

したがって適切な組合せは a1＝true、a2＝true です。

∴a＝エ

〔bについて〕
関数 calcCheckCharacter の返却値として getChar(check_value) が指定されていることから、変数 check_value は検査文字に対応する数値とわかります。
問題文では求めた総和から検査文字を算出するプロセスについて以下のように説明されています。

「Nから，③で求めた総和をNで割った余りを引く。さらにその結果を，Nで割り，余りを求める。求めた数値に対応する文字を検査文字とする」

ループ処理によって総和は変数 sum に求められています。「A % B」はAをBで割った余り(剰余算)を表すので、「%」を使い、説明をそのまま式にすると以下のようになります。
pm08_10.png
∴b＝ウ：(N - sum % N) % N

以下はこの問題の checkCheckCharacter と validateCheckCharacter をJavascriptで実装したものです。細かな動作の確認等にお使いください。


〔cについて〕
関数 validateCheckCharacter は返却値がtrueならば"誤りなし"、falseであれば"誤りあり"と判定します。c＝trueならば返却値である ret_value にfalseが設定されるため、cには"誤りあり"と判定するための条件式が入ります。
問題文では求めた総和から正誤を判定するプロセスについて以下のように説明されています。

「③で求めた総和がNで割り切れる場合は，検査文字付文字列に誤りがないと判定する。Nで割り切れない場合は，検査文字付文字列に誤りがあると判定する」

つまりsumがNで割り切れないときに"誤りあり"と判定されます。割り切れないときにはsum÷Nの余りがゼロではないので、cには条件式「sum % N≠ 0」が入ります。

∴c＝エ：sum % N ≠ 0
広告

設問2

次の記述中の　に入れる正しい答えを，解答群の中から選べ。

　本プログラムでは，検査文字付文字列の誤りが1文字であれば，誤りを検出できる。しかし，複数の文字に誤りがある場合には，誤りがないと判定されることがある。例えば，関数 validateCheckCharacter で表4に示す検査文字付文字列を検証した場合，誤りがないと判定されるケースはd。ここで，文字列ipa␣␣に対し生成される検査文字は f である。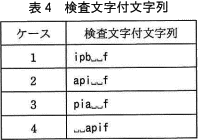
pm08_6.png
d に関する解答群
  • 1と2と3と4である
  • 2である
  • 2と3である
  • 2と3と4である
  • 2と4である
  • ない
解答選択欄
  • d:
  • d=オ

解説

総和を求める過程では、奇数番目と偶数番目で適用される処理が異なります。しかし1番目と3番目と奇数番目同士、2番目と4番目というように偶数番目同士の文字が入れ替わっても算出される総和は同じになります。総和が同じならば元の文字列と異なっても"誤りなし"と判定されてしまいます。

ipa␣␣では、後ろから1,3,5番目の[␣,a,i]が同じ組、2,4番目の[␣,p]が同じ組になり、同じ計算処理が適用されます。つまり、この組の中での文字の入れ替えであれば総和は同じになります。
  • aのところにbが入っています。文字が変わると総和も変わるため"誤りあり"と判定されます。
  • 元の文字列と比較してiとaが入れ替わっています。iとaは同じ組なので算出される総和は元の文字列と同じになり、結果は"誤りなし"と判定されます。
  • 元の文字列と比較してiとpが入れ替わっています。iとpは同じ組ではないので算出される総和は元の文字列と異なり、結果は"誤りあり"と判定されます。
  • 元の文字列と比較してiと␣、pと␣が入れ替わっています。iと␣、pと␣はそれぞれ同じ組なので算出される総和は元の文字列と同じになり、結果は"誤りなし"と判定されます。
したがって"誤りなし"と判定されるケースは2と4の2つです。

∴d＝オ：2と4である
広告

設問3

次の記述中の　に入れる正しい答えを，解答群の中から選べ。

　本プログラムを文字列長が同じである複数の文字列に対して適用することを考える(図1参照)。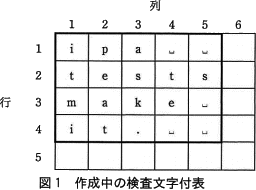
pm08_7.png
〔考え方〕
　文字列長がnであるm個の文字列について考える。文字列に対して，(m＋1)行(n＋1)列の表を用意する。以後，この表を検査文字付表という。
  • 検査文字の生成
    　例えば，文字列長が5である4個の文字列ipa␣␣，tests，make␣，it.␣␣を，図1の太枠内のように，各文字列の先頭の位置を最左列に揃え，各文字列を上の行から順に格納して，表を作成する。この表の太枠内の各行各列をそれぞれ文字列とみなして検査文字を生成し，最右列と最下行に格納する。
    　この手順で作成した検査文字付表を図2に示す。作成した検査文字付表の5行5列目(網掛け部分)の検査文字はeである。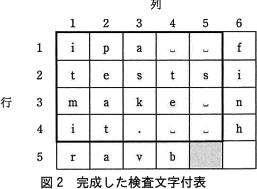
    pm08_8.png
  • 検査文字付表の検証
    　(1)で作成した検査文字付表の，最下行を除く各行と最右列を除く各列を文字列とみなし，それぞれ関数 validateCheckCharacter で検証した結果，全て誤りがないと判定された場合には，検査文字付表に誤りがないと判定する。一つでも誤りがあると判定された場合は，検査文字付表に誤りがあると判定する。
e に関する解答群
  • j
  • k
  • l
  • m
解答選択欄
  • e:
  • e=ウ

解説

〔eについて〕
表の網掛け部分には、5列目の文字列 ␣s␣␣ に対応する検査文字が入ります。検査文字の生成手順に従って検査文字を算出します。
  • ␣ → 0×2÷30＝0 余り 0
  • ␣ → 0
  • s→ 22×2÷30＝1 余り 14
  • ␣ → 0
　総和＝0＋0＋15＋0＝15

総和(=15)をNで割った余りを求め、Nから引きます。さらにその結果をNで割った余りが検査文字です。
  • 15÷30＝0 余り 15
  • 30－15＝15
  • 15÷30＝0 余り 15
  • 15 → l //検査文字はl
∴e＝ウ：l
広告

設問4

次の記述中の　に入れる正しい答えを，解答群の中から選べ。

　図2の1行目の検査文字付文字列を取り除いた，図3の検査文字付表について考える。表4のケース1～4の検査文字付文字列を順に，図3の1行目に格納して検証した場合，検査文字付表に誤りがないと判定されるケースはf。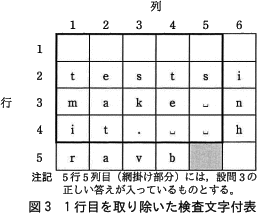
pm08_9.png
f に関する解答群
  • 1と2と3と4である
  • 2である
  • 2と3である
  • 2と3と4である
  • 2と4である
  • ない
解答選択欄
  • f:
  • f=カ

解説

表の第1行目は第5行目から数えて5番目(奇数番目)なので、検査文字検証のプロセスにおいて文字に対応する数値をそのまま総和(sum)に加算します。数値と文字は一意に関連付けられているので、各列の検査文字付文字列が"誤りなし"と判定される(=Nで割り切れる)ためには、元の文字と同じ文字である必要があります。すなわち検査表全体に誤りがないと判定されるのはipa␣␣のみであり、1～4の中に該当するケースはありません。

∴f＝カ：ない
広告
広告

前の問題次の問題

▲
Pagetop