平成29年春期試験問題　午前問1

午前試験免除制度対応！基本情報技術者試験のeラーニング【独習ゼミ】
問1解説へ
集合A，B，Cを使った等式のうち，集合A，B，Cの内容によらず常に成立する等式はどれか。ここで，∪は和集合，∩は積集合を示す。

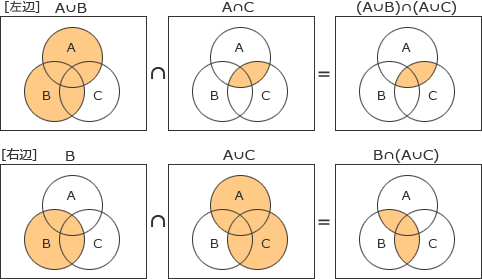
  • (A∪B)∩(A∩C) ＝ B∩(A∪C)
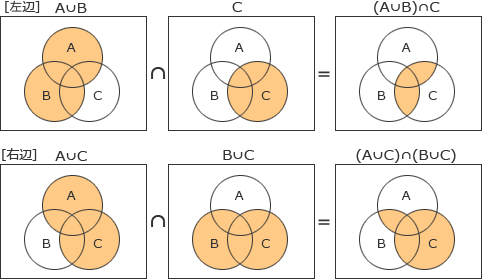
  • (A∪B)∩C ＝ (A∪C)∩(B∪C)
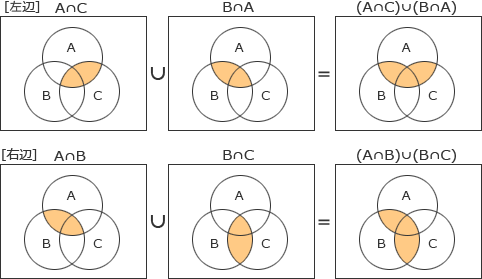
  • (A∩C)∪(B∩A) ＝ (A∩B)∪(B∩C)
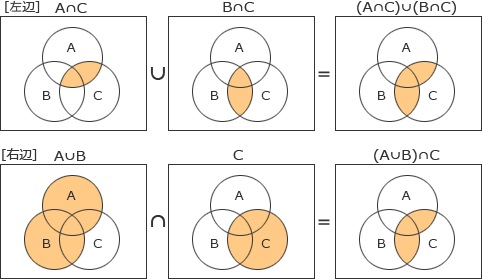
  • (A∩C)∪(B∩C) ＝ (A∪B)∩C
正解　エ問題へ
分野：テクノロジ系
中分類：基礎理論
小分類：離散数学
広告
解説
少し手間はかかりますが論理式をベン図で表して比較する方法が確実です。
  • 01a.png
  • 01i.png
  • 01u.png
  • 01e.png
左辺と右辺の集合が完全一致する「エ」が正解です。

また最速で正解を導く方法は集合演算の"分配の法則"を使用することでしょう。
分配の法則
A∪(B∩C)＝(A∪B)∩(A∪C)
A∩(B∪C)＝(A∩B)∪(A∩C)
これを適用すれば「エ」が同一の式であるとすぐにわかります。

　(A∩C)∪(B∩C) → (A∪B)∩C
広告

次の問題

▲
Pagetop