平成30年春期試験午後問題 問2

問2 ハードウェア
論理回路に関する次の記述を読んで,設問1~3に答えよ。
主要な論理演算の真理値表を表1に示す。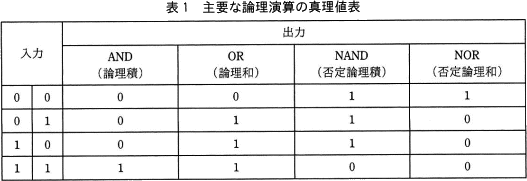
主要な論理演算の真理値表を表1に示す。

広告
設問1
表1に示した論理演算を行う論理回路を用いて,表2に示すXOR(排他的論理和)の論理演算を行う論理回路を図1のとおり作成した。図1中の に入れる正しい答えを,解答群の中から選べ。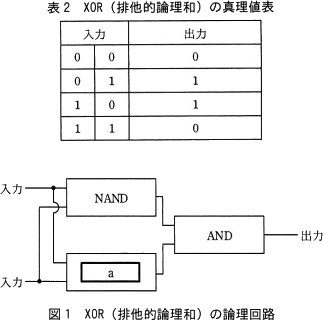

a に関する解答群
- AND
- NAND
- NOR
- OR
解答選択欄
- a:
- a=エ
解説
図1の回路図における、2つの入力の組合せとNAND回路及びaの出力、そして全体の出力の関係を整理すると下図のようになります。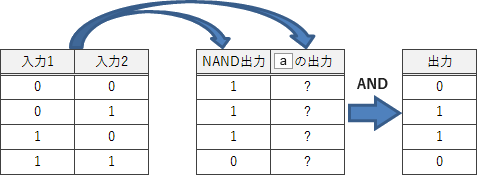
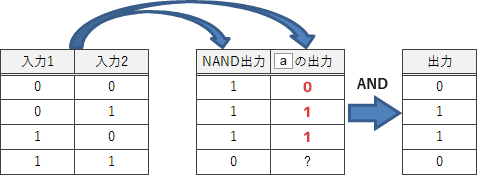
∴a=エ:OR
広告
設問2
1桁の2進数X,Yを入力して,その和の下位桁をZ,桁上がりをCに出力する半加算器の論理回路を図2に示す。図2中の に入れる正しい答えを,解答群の中から選べ。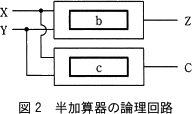

b,c に関する解答群
- AND
- NAND
- NOR
- OR
- XOR
解答選択欄
- b:
- c:
- b=オ
- c=ア
解説
半加算器における、2つの入力値及び出力Cと出力Zの関係を図示すると以下のようになります。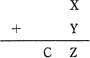
出力Zは下位桁を表すビットです。2つの入力値と出力Zの間には以下の関係があります。
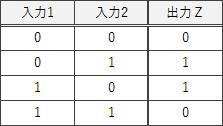
∴b=オ:XOR
〔cについて〕
出力Cは桁上がりを表すビットです。2つの入力値と出力Cの間には以下の関係があります。
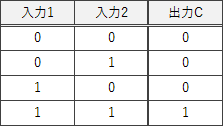
∴c=ア:AND
広告
設問3
論理回路に関する次の記述中の に入れる正しい答えを,解答群の中から選べ。
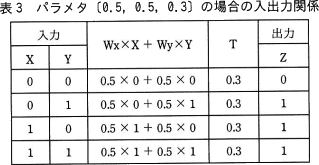
この論理回路は,1ビットの入力 X,Y をそれぞれパラメータ Wx,Wy で重み付けして加算した結果を求め,パラメータ T をしきい値として,次のとおりに動作する。
 同様に,
同様に,
この論理回路は,1ビットの入力 X,Y をそれぞれパラメータ Wx,Wy で重み付けして加算した結果を求め,パラメータ T をしきい値として,次のとおりに動作する。
- Wx×X+Wy×Y≧Tのとき,1をZに出力する。
- Wx×X+Wy×Y<Tのとき,0をZに出力する。

- AND(論理積)になる入出力関係は,パラメータdで実現できる。
- NAND(否定論理積)になる入出力関係は,パラメータeで実現できる。
d,e に関する解答群
- 〔-0.5,-0.5,-0.8〕
- 〔-0.5,-0.5,-0.2〕
- 〔0.5,0.5,-0.5〕
- 〔0.5,0.5,0.2〕
- 〔0.5,0.5,0.8〕
- 〔0.5,0.5,1.5〕
解答選択欄
- d:
- e:
- d=オ
- e=ア
解説
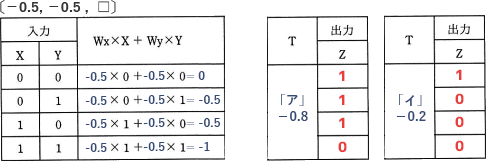
各パラメータを使用して図3と同様に計算していきます。重みのパラメータ(WxとWy)の組合せは2種類しかありませんので、まずそれぞれの「Wx×X+Wy×Wy」を計算してから、しきい値Tの違いによる出力値の変化を見極める方法が良さそうです。[重みパラメータが〔-0.5,-0.5,□〕]
[重みパラメータが〔0.5,0.5,□〕]
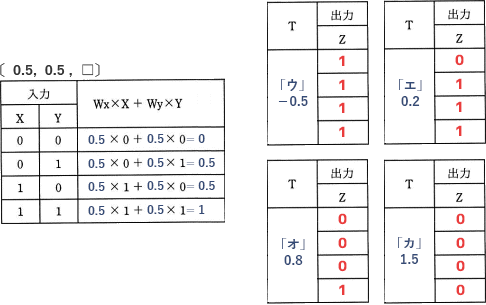
- NANDの真理値表と一致します。よってeには「ア」のパラメータが入ります。
- NORの真理値表と一致します。
- 全ての出力が"1"となる論理回路です。
- ORの真理値表と一致します。
- ANDの真理値表と一致します。よってdには「オ」のパラメータが入ります。
- 全ての出力が"0"となる論理回路です。
e=ア:〔-0.5,-0.5,-0.8〕
広告
広告