分野 ：テクノロジ系
中分類：基礎理論
小分類：応用数学

標準偏差は、数値データ群の散らばり度合いを表すものです。次のように求めます。

1. x1, x2, x3, ... , xn のn個の数値データの平均を μ とする
2. データごとにμとの差（偏差）の2乗を求め、合計する。これを分散と呼ぶ
3. 分散は元データを2乗しているため、平方根を求めることで元データと単位を揃える。この分散を標準偏差と呼ぶ

設問では、①全てのデータに対して定数aを加えた場合、②全てのデータを2倍した場合の標準偏差が問われています。それぞれ検討します。

①全てのデータに対して定数aを加えた場合

全てのデータに定数aを加えると、平均もaだけ高くなります。データ群全体がaだけ移動しますが、分布の形状は変わらないため散らばり度合いは変化しません。したがって、標準偏差は元のデータ群と同じになります

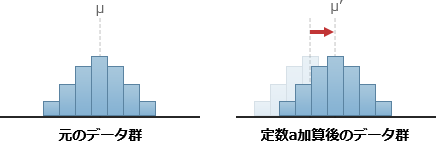
②全てのデータを2倍した場合

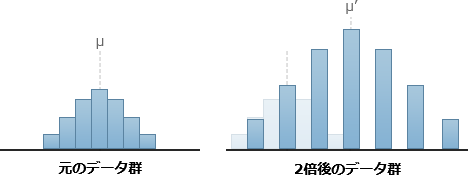
全てのデータを2倍すると、1, 2, 3 ⇒ 2, 4, 6 というようにデータ同士の差も2倍となります。分布の形状が広がるので、散らばり度合いが大きくなります。このとき各データの偏差も2倍となるため、標準偏差は元のデータ群の2倍になります

• 元の標準偏差と同じになります。
• 元の標準偏差と同じになります。
• 元の標準偏差の2倍になります。
• 正しい。元の標準偏差の2倍になります。