分野：テクノロジ系
中分類：基礎理論
小分類：応用数学

すべての経路を表すと下図のとおりです。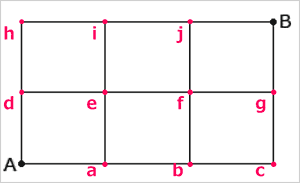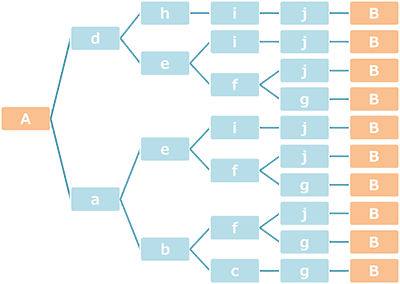※最短経路なので、B地点から遠ざかる経路は選ばないこと

計算で求める場合は、コンビネーション（組み合わせ）を考えます。
まず、縦と横の区画数を数えます。

　縦：2区画
　横：3区画

つまり、いずれの経路を通ったとしてもA地点からB地点までの経路は、縦2区画、横3区画なので以下のように表せます。

　縦→縦→横→横→横
　縦→横→縦→横→横
　縦→横→横→縦→横
　縦→横→横→横→縦
　…

縦を基準にして考えると、5つから2つを選ぶ組み合わせを求めると…

_(縦＋横)C_縦

で、最短経路を求めることができます。

　₅C₂＝(5×4)÷(2×1)＝10

または、横を基準にして考えると、5つから3つを選ぶ組み合わせを求めると…

　_(縦＋横)C_横

で、最短経路を求めることができます。

　₅C₃＝(5×4×3)÷(3×2×1)＝10

したがって、正解は「イ」です。