応用数学 (全50問中15問目)
No.15
次の例に示すように，関数ƒ(x)はx以下で最大の整数を表す。
ƒ(1.0)＝1
ƒ(0.9)＝0
ƒ(－0.4)＝－1
小数点以下1桁の小数－0.9，－0.8，…，－0.1，0.0，0.1，…，0.8，0.9からxを等確率で選ぶとき，ƒ(x＋0.5)の期待値(平均値)は幾らか。
ƒ(1.0)＝1
ƒ(0.9)＝0
ƒ(－0.4)＝－1
小数点以下1桁の小数－0.9，－0.8，…，－0.1，0.0，0.1，…，0.8，0.9からxを等確率で選ぶとき，ƒ(x＋0.5)の期待値(平均値)は幾らか。
出典：平成27年春期 問3
- －120
- 0
- 120
- 119
分類
テクノロジ系 » 基礎理論 » 応用数学
正解
エ
解説
xには－0.9～0.9までの値が入る可能性があるので、x＋0.5は、最小値が－0.4、最大値が1.4の変域をとります。
それぞれの場合を ƒ(x＋0.5) の結果ごとに分類すると、以下のようになります。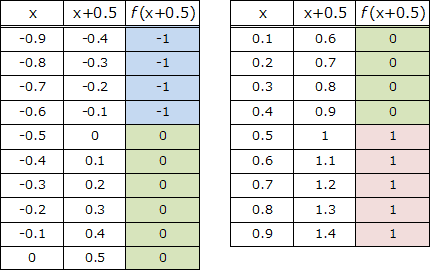
期待値は以下のように計算できます。
－1×4＋0×10＋1×519
＝－4＋519＝119
したがって「エ」が正解です。
それぞれの場合を ƒ(x＋0.5) の結果ごとに分類すると、以下のようになります。
- －1 … －0.4～－0.1までの4つ
- 0 … 0.0～0.9までの10つ
- 1 … 1.0～1.4までの5つ
－1×4＋0×10＋1×519
＝－4＋519＝119
したがって「エ」が正解です。