応用数学 (全50問中28問目)
No.28
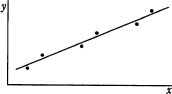
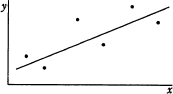
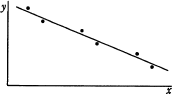
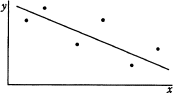
標本相関係数が-0.9,-0.7,0.7,0.9のいずれかとなる標本の分布と回帰直線を表したグラフのうち,標本相関係数が-0.9のものはどれか。
出典:平成20年春期 問8
分類
テクノロジ系 » 基礎理論 » 応用数学
正解
ウ
解説
相関係数は、2つの項目の関連度合いを示す値です。値として-1~+1の間の実数値をとり、-1に近ければ負の相関があり回帰直線は右肩下がり、+1に近ければ正の相関があり回帰直線は右肩上がりを描きます。値が0に近いときには2項目間の相関は弱いと判断されます。
負の相関といっても、正に比べて関連性が弱いわけではありません。正負の方向は相関の強さには関係なく、より相関係数の絶対値が(1に近い)大きいものが強い相関性をもつことを表します。
標本相関係数-0.9は負の相関ということになるので、選択肢の中で「ウ」と「エ」が候補となります。もう一方のグラフの標本相関係数は-0.7ということが問題文からわかっているので、2つのグラフのうちより2項目間の相関性が高い「ウ」のグラフが標本相関係数-0.9の回帰直線を表したグラフになります。
負の相関といっても、正に比べて関連性が弱いわけではありません。正負の方向は相関の強さには関係なく、より相関係数の絶対値が(1に近い)大きいものが強い相関性をもつことを表します。
標本相関係数-0.9は負の相関ということになるので、選択肢の中で「ウ」と「エ」が候補となります。もう一方のグラフの標本相関係数は-0.7ということが問題文からわかっているので、2つのグラフのうちより2項目間の相関性が高い「ウ」のグラフが標本相関係数-0.9の回帰直線を表したグラフになります。