離散数学 (全109問中32問目)
No.32
論理式 A・B・C＋A・B・C＋A・B・C＋A・B・C と恒等的に等しいものはどれか。ここで，・は論理積，＋は論理和，AはAの否定を表す。
出典：平成26年春期 問3
- A・B・C
- A・B・C＋A・B・C
- A・B＋B・C
- C
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
エ
解説
ベン図を使用して解く方法と論理式の変形で解く方法の2通りを紹介します。
[ベン図]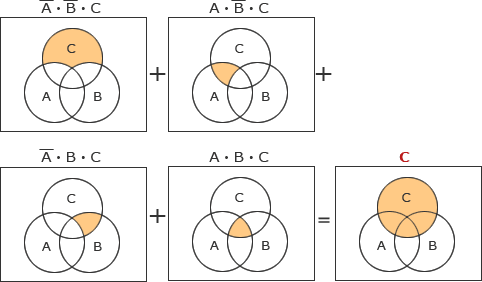
[論理式の変形]
A・B・C＋A・B・C＋A・B・C＋A・B・C
＝C・(A・B＋A・B＋A・B＋A・B) //分配の法則
＝C・(B・(A＋A)＋B・(A＋A)) //分配の法則
＝C・(B＋B) //A＋A＝1
＝C //B＋B＝1
したがって設問の論理式と等しいのは「C」になります。
[ベン図]
A・B・C＋A・B・C＋A・B・C＋A・B・C
＝C・(A・B＋A・B＋A・B＋A・B) //分配の法則
＝C・(B・(A＋A)＋B・(A＋A)) //分配の法則
＝C・(B＋B) //A＋A＝1
＝C //B＋B＝1
したがって設問の論理式と等しいのは「C」になります。