離散数学 (全109問中4問目)
No.4
nビットの値 L1,L2がある。次の操作によって得られる値L3は,L1とL2に対するどの論理演算の結果と同じか。
〔操作〕
〔操作〕
- L1とL2のビットごとの論理和をとって,変数Xに記憶する。
- L1とL2のビットごとの論理積をとって更に否定をとり,変数Yに記憶する。
- XとYのビットごとの論理積をとって,結果をL3とする。
出典:令和3年免除 問1
- 排他的論理和
- 排他的論理和の否定
- 論理積の否定
- 論理和の否定
- [出典]
- 午前免除試験 R3-12月 問1
- 応用情報技術者 H28 問1と同題
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
ア
解説
ビット列L1=10101010,ビット列L2=11110000 を例として操作の様子を確認していきます。
[操作(1)]
2つのビット列の論理和なので、2つのビットの一方または双方が"1"になっている部分を"1"としたビット列が変数Xに格納されます。 [操作(2)]
[操作(2)]
2つのビット列の論理積の否定なので、2つのビットがともに"1"ある部分以外を"1"としたビット列が変数Yに格納されます。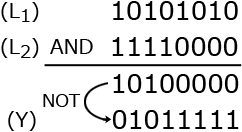 [操作(3)]
[操作(3)]
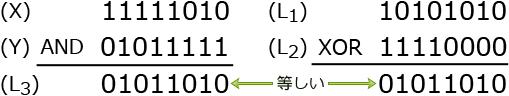 したがって正解は「ア」です。
したがって正解は「ア」です。
【別解】
変数X、変数Yの集合をベン図で表し、両者の論理積をとった結果の集合を見て、適合する論理演算を判断します。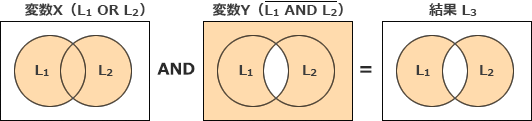
[操作(1)]
2つのビット列の論理和なので、2つのビットの一方または双方が"1"になっている部分を"1"としたビット列が変数Xに格納されます。

2つのビット列の論理積の否定なので、2つのビットがともに"1"ある部分以外を"1"としたビット列が変数Yに格納されます。
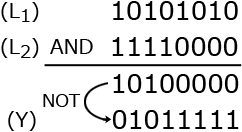
- 変数X
- 2つのビットの一方または双方が"1"の部分が"1"
- 変数Y
- 2つのビットがともに"1"の部分以外が"1
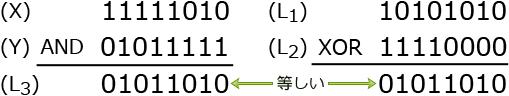
【別解】
変数X、変数Yの集合をベン図で表し、両者の論理積をとった結果の集合を見て、適合する論理演算を判断します。

