離散数学 (全109問中41問目)
No.41
10進数-5.625を，8ビット固定小数点形式による2進数で表したものはどれか。ここで，小数点位置は3ビット目と4ビット目の間とし，負数には2の補数表現を用いる。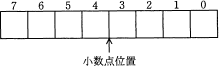
出典：平成23年秋期 問2
- 01001100
- 10100101
- 10100110
- 11010011
- [出題歴]
- ソフトウェア開発技術者 H13春期 問2
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
ウ
解説
2進数の各桁と10進数の関係は下図のようになっています。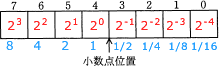
まず正数の5.625を2進数で求め、その後、求めたビット列を2の補数表現にすることで-5.625を2進数に変換します。
整数部の"5"は 4＋1と表せるので、22＋20→0101(2)，小数部の"0.625"は 0.5＋0.125と表せるので、2-1＋2-3→0.1010(2)となり、この二つを足し合わせた0101.1010(2)が5.625の8ビット固定小数点形式ということになります。
10進数-5.625は負数なので、正数の5.625(2進数では0101.1010)を2の補数で表現したものになります。あるビット列の2の補数は、すべてのビットを反転し、最下位ビットに1を加えることで求められるので、
0101.1010を反転→1010.0101
1010.0101の最下位ビットに1を加える→1010.0110
したがって正解は「1010.0110」になります。
整数部の"5"は 4＋1と表せるので、22＋20→0101(2)，小数部の"0.625"は 0.5＋0.125と表せるので、2-1＋2-3→0.1010(2)となり、この二つを足し合わせた0101.1010(2)が5.625の8ビット固定小数点形式ということになります。
10進数-5.625は負数なので、正数の5.625(2進数では0101.1010)を2の補数で表現したものになります。あるビット列の2の補数は、すべてのビットを反転し、最下位ビットに1を加えることで求められるので、
0101.1010を反転→1010.0101
1010.0101の最下位ビットに1を加える→1010.0110
したがって正解は「1010.0110」になります。