離散数学 (全109問中79問目)
No.79
次の真理値表で,変数X,Y,Zに対する関数Fを表す式はどれか。ここで,“・”は論理積,“+”は論理和,AはAの否定を表す。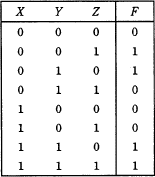

出典:平成18年秋期 問9
- X・Y+Y・Z
- X・Y・Z+Y
- X・Y・Z+X・Y+Y・Z
- X・Y・Z+X・Y+Y・Z
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
ウ
解説
X,Y,Zに適当な値を代入して、その結果が真理値表と同じになるかを検証していきます。結果の値が分かれそうな組合せならどれでも良いのですが、この解説では[X=0,Y=0,Z=1,F=1]の組合せを用いることとします。
[X=1,Y=0,Z=1,F=0]
- 0・0+0・1
=0・0+0・0
=0+0=0
結果が真理値表と異なるので誤りとわかります。 - 0・0・1+0
=0・0・0+0
=0+0=0
結果が真理値表と異なるので誤りとわかります。 - 0・0・1+0・0+0・1
=1・1・1+0・0+0・0
=1+0+0=1
結果が真理値表と同じなので正しい可能性があります。 - 0・0・1+0・0+0・1
=1・1・1+0・1+1・0
=1+0+0=1
結果が真理値表と同じなので正しい可能性があります。
[X=1,Y=0,Z=1,F=0]
- 「ウ」
1・0・0+1・0+0・0
=0・1・0+1・0+0・1
=0+0+0=0
結果が真理値表と同じなので正しい可能性があります。 - 「エ」
1・0・0+1・0+0・0
=0・1・0+1・1+1・1
=0+1+1=1
結果が真理値表と異なるので誤りとわかります。
