HOME»基本情報技術者令和6年»[科目B]問3
基本情報技術者令和6年 [科目B]問3
問3
次のプログラム中の に入れる正しい答えを，解答群の中から選べ。ここで，配列の要素番号は1から始まる。
図1に示すグラフの頂点には，1から順に整数で番号が付けられている。グラフは無向グラフであり，各頂点間には高々一つの辺がある。一つの辺は両端の頂点の番号を要素にもつ要素数2の整数型の配列で表現できる。例えば，{1，3}は頂点1と頂点3を端点とする辺を表す。グラフ全体は，グラフに含まれる辺を表す要素数2の配列を全て格納した配列(以下，辺の配列という)で表現できる。辺の配列の要素数はグラフの辺の個数と等しい。図1のグラフは整数型配列の配列{{1，3}，{1，4}，{3,4}，{2，4}，{4，5}}と表現できる。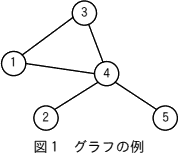
関数 edgesToMatrix は，辺の配列を隣接行列に変換する。隣接行列とは，グラフに含まれる頂点の個数と等しい行数及び列数の正方行列で，i行j列の成分は頂点iと頂点jを結ぶ辺があるときに1となり，それ以外は0となる。行列の対角成分は全て0で，無向グラフの場合は対称行列になる。図1のグラフを表現する隣接行列を図2に示す。
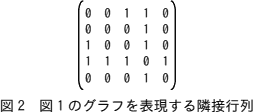関数 edgesToMatrix は，引数 edgeList で辺の配列を，引数 nodeNum でグラフの頂点の個数をそれぞれ受け取り，隣接行列を表す整数型の二次元配列を返す。
〔プログラム〕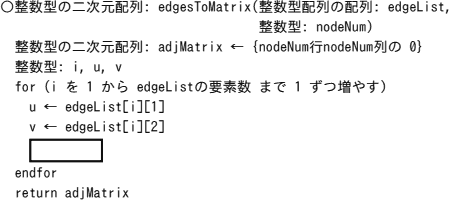
図1に示すグラフの頂点には，1から順に整数で番号が付けられている。グラフは無向グラフであり，各頂点間には高々一つの辺がある。一つの辺は両端の頂点の番号を要素にもつ要素数2の整数型の配列で表現できる。例えば，{1，3}は頂点1と頂点3を端点とする辺を表す。グラフ全体は，グラフに含まれる辺を表す要素数2の配列を全て格納した配列(以下，辺の配列という)で表現できる。辺の配列の要素数はグラフの辺の個数と等しい。図1のグラフは整数型配列の配列{{1，3}，{1，4}，{3,4}，{2，4}，{4，5}}と表現できる。
〔プログラム〕
- adjMatrix[u，u] ← 1
- adjMatrix[u，u] ← 1
adjMatrix[v，v] ← 1 - adjMatrix[u，v] ← 1
- adjMatrix[u，v] ← 1
adjMatrix[v，u] ← 1 - adjMatrix[v，u] ← 1
- adjMatrix[v，v] ← 1
分類
アルゴリズムとプログラミング » データ構造及びアルゴリズム
正解
エ
解説
図1のグラフの配列表現 {{1, 3}, {1, 4}, {3, 4}, {2, 4}, {4, 5}}と図2の隣接行列は次のように対応します。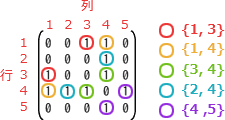
二次元配列 adjMatrix は上記の隣接行列を表したものなので、{1, 3}の配列要素であれば adjMatrix の [1, 3] および [3, 1] を1に、同様に{1, 4}の配列要素であれば [1, 4] および [4, 1] を1にすれば良いことがわかります。つまり、1つの辺を表すためには、二次元配列の [行番号, 列番号]、[列番号, 行番号] の2つの場所を1にする必要があるということです。
for文の処理では、辺の配列である edgeList の要素に順番にアクセスし、その1番目の要素を変数 u に、2番目の要素を変数 v に格納しています。先頭要素である{1, 3}を例に出すと、変数 u には1(行番号)が、変数 v には3(列番号)が格納されることになります。配列表現と隣接行列の対応関係を踏まえると、[行番号, 列番号] は [u, v]、[列番号, 行番号] は [v, u] と変数で表すことができます。 この2つの場所にそれぞれ1を代入することで、1つの辺を表すことができます。
for文の処理では、辺の配列である edgeList の要素に順番にアクセスし、その1番目の要素を変数 u に、2番目の要素を変数 v に格納しています。先頭要素である{1, 3}を例に出すと、変数 u には1(行番号)が、変数 v には3(列番号)が格納されることになります。配列表現と隣接行列の対応関係を踏まえると、[行番号, 列番号] は [u, v]、[列番号, 行番号] は [v, u] と変数で表すことができます。 この2つの場所にそれぞれ1を代入することで、1つの辺を表すことができます。
- adjMatrix[u，v] ← 1
- adjMatrix[v，u] ← 1