HOME»Pythonサンプル問題
基本情報技術者試験 Pythonサンプル問題
Pythonのプログラムに関する次の記述を読んで,設問1,2に答えよ。
命令列を解釈実行することによって様々な図形を描くプログラムである。
命令列を解釈実行することによって様々な図形を描くプログラムである。
- 描画キャンバスの座標は,x軸の範囲が-320~320,y 軸の範囲が-240~240である。描画キャンバスの座標系を,図1に示す。描画キャンバス上にはマーカがあり,マーカを移動させることによって描画する。マーカは,現在の位置座標と進行方向の角度を情報としてもつ。マーカの初期状態の位置座標は(0,0)であり,進行方向はx軸の正方向である。

- 命令列は,命令を";"で区切った文字列である。命令は,1文字の命令コードと数値パラメタの対で構成される。命令には,マーカに対して移動を指示する命令,マーカに対して回転を指示する命令,及び命令列中のある範囲の繰返しを指示する命令がある。繰り返す範囲を,繰返し区間という。命令は,命令列の先頭から順に実行する。命令とその説明を,表1に示す。

- 命令列 R3;R4;F100;T90;E0;F100;E0 (以下,命令列αという)の繰返し区間を,図2に示す。マーカが初期状態にあるときに,命令列αを実行した場合の描画結果を,図3に示す。
なお,図3中の描画キャンバスの枠,目盛りとその値,①,② 及び矢印は,説明のために加えたものである。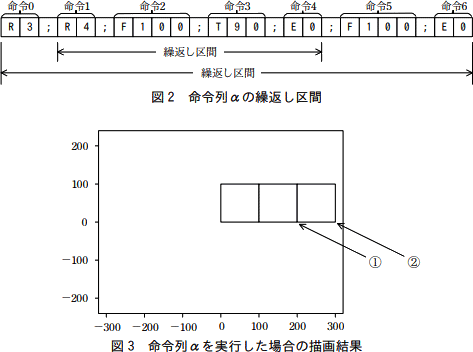
設問1
次の記述中の に入れる正しい答えを,解答群の中から選べ。ここで,a1とa2に入れる答えは,aに関する解答群の中から組合せとして正しいものを選ぶものとする。
- 命令列αの実行が終了した時点でのマーカの位置は,図3中のa1が指す位置にあり,進行方向はa2である。
- マーカが初期状態にあるときに,図4に示す1辺の長さが100の正五角形を描くことができる命令列は,bである。ここで,図4中の描画キャンバスの枠,目盛りとその値は,説明のために加えたものである。

a に関する解答群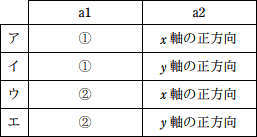

b に関する解答群
- R5;F100;T-108;E0
- R5;F100;T-75;E0
- R5;F100;T-72;E0
- R5;F100;T-60;E0
- R5;F100;T60;E0
- R5;F100;T72;E0
- R5;F100;T75;E0
- R5;F100;T108;E0
解答選択欄
- a:
- b:
解答
- a=ウ
- b=カ
解説
〔aについて〕
図2「命令列αの繰返し区間」では繰返し処理が二重になっています。これをプログラムの構造として見ると次のように命令が実行されていくことになります。
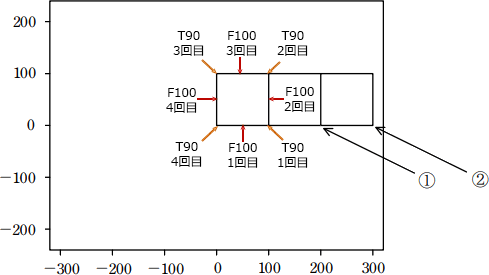 そして内側の繰返し処理が終わった後に、外側の繰返しで F100 が実行されると、マーカの位置が100だけ右に移動します。つまり、外側の繰返しが1回終わると正方形が描かれ、描いた正方形の右下頂点の位置にマーカが移動していることになります。
そして内側の繰返し処理が終わった後に、外側の繰返しで F100 が実行されると、マーカの位置が100だけ右に移動します。つまり、外側の繰返しが1回終わると正方形が描かれ、描いた正方形の右下頂点の位置にマーカが移動していることになります。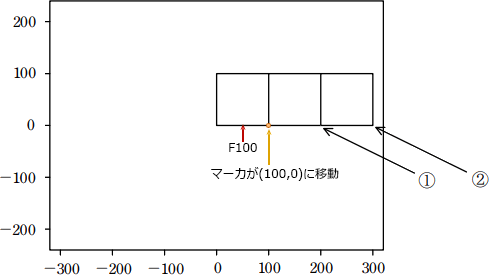 これを3回繰り返すので、命令列α実行後のマーカの位置は3個目に描いた正方向の右下頂点である②にあり、マーカは右方向(x軸の正方向)を向いています。
これを3回繰り返すので、命令列α実行後のマーカの位置は3個目に描いた正方向の右下頂点である②にあり、マーカは右方向(x軸の正方向)を向いています。
したがって、a1=②、a2=x軸の正方向 となる「ウ」の組合せが適切です。
∴a=ウ
〔bについて〕
正方形を描いた時と同じように考えると、進行方向に進むことと、反時計回りに回転する動作を5回繰り返すと正五角形を描けます。線分の長さはどの選択肢も100となっているので、問題となるのは角度と方向を記述するT命令の数値パラメタになります。
∴b=カ:R5;F100;T72;E0
※正五角形の1つの内角を「540÷5=108」で求め、「180-108=72」で計算することも可能です。
図2「命令列αの繰返し区間」では繰返し処理が二重になっています。これをプログラムの構造として見ると次のように命令が実行されていくことになります。
(F100;T90;)×4回
F100
(F100;T90)×4回
F100
(F100;T90;)×4回
F100
内側の繰返し区間は F100;T90 の命令を4回繰り返します。表1「命令とその説明」を見ると、各命令は以下の動作をすることがわかります。F100
(F100;T90)×4回
F100
(F100;T90;)×4回
F100
- F100
- マーカの進行方向に100進んで線分を描く
- T90
- マーカの進行方向を反時計回りに90度回転する


したがって、a1=②、a2=x軸の正方向 となる「ウ」の組合せが適切です。
∴a=ウ
〔bについて〕
正方形を描いた時と同じように考えると、進行方向に進むことと、反時計回りに回転する動作を5回繰り返すと正五角形を描けます。線分の長さはどの選択肢も100となっているので、問題となるのは角度と方向を記述するT命令の数値パラメタになります。
- 数値パラメタの正負
- 先程と同じように反時計回りに回転させたいので"正"です。
- 回転させる角度
- 正N角形の外角の大きさは「360÷N」で計算できるので、正五角形の外角の大きさは「360÷5=72度」です※。
∴b=カ:R5;F100;T72;E0
※正五角形の1つの内角を「540÷5=108」で求め、「180-108=72」で計算することも可能です。
〔プログラムの説明〕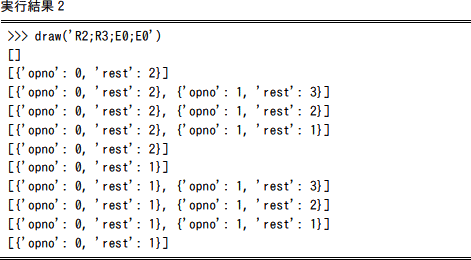

- 関数 parse は,引数として与えられた命令列を,タプルを要素とするリストに変換する。ここで,命令列は,少なくとも一つの命令をもち,誤りはないものとする。1タプルは,1命令に相当し,命令コード及び数値パラメタから構成される。関数 parse が定義された状態での,対話モードによる実行例を,実行結果1に示す。

- クラス Marker は,マーカの現在の位置座標を属性x,y に,進行方向をx軸正方向から反時計回りに測った角度で属性 angle に保持する。オブジェクトの生成時に,描画キャンバスの表示範囲を設定し,属性x,yを0,0に,属性 angle を0に設定する。クラス Marker に,マーカの操作をする次のメソッドを定義する。
- forward(val)
- マーカの位置座標を,現在の進行方向に val で指定された長さだけ進め,線分を描く。
引数:val 長さ - turn(val)
- マーカの進行方向を,反時計回りに val で指定された角度だけ回転させる。
引数:val 度数法で表した角度
- 関数 draw は,引数として与えられた命令列の各命令を解釈実行し,描画結果を表示する。ここで,命令列は,少なくとも一つの命令をもち,誤りはないものとする。関数 draw の概要を,次に示す。
- 命令列を,関数 parse を利用してタプルを要素とするリストに変換する。
- マーカの操作は,クラス Marker を利用する。
- 繰返し区間の入れ子を扱うために,スタックを用いる。
- スタックはリストで表現され,各要素は繰返しの開始位置 opno と残り回数 rest をもつ辞書である。
- プログラムの位置βにある print 関数を使って,スタックの状態変化を出力する。


設問2
プログラム中の に入れる正しい答えを,解答群の中から選べ。ここで,d1とd2に入れる答えは,dに関する解答群の中から組合せとして正しいものを選ぶものとする。dに関する解答群の中で使用される標準ライブラリの仕様は,次のとおりである。
- math.sin(x)
- 指定された角度の正弦(sin)を返す。
引数:x ラジアンで表した角度
戻り値:引数の正弦(sin) - math.cos(x)
- 指定された角度の余弦(cos)を返す。
引数:x ラジアンで表した角度
戻り値:引数の余弦(cos)
c に関する解答群
- int(x[1])
- int(x[1:])
- int(x[:1])
- int(x[2])
- int(x[2:])
- int(x[:2])
d に関する解答群

e に関する解答群
- 0, 0
- dx, dy
- self.x, self.y
- self.x - dx, self.y - dy
f に関する解答群
- 0
- code
- len((insts)
- val
g に関する解答群
- < 0
- < 1
- == 0
- > 0
- > 1
h,i に関する解答群
- opno = stack[-1]['opno']
- stack.clear() # stack をクリア
- stack.pop() # stack の末尾の要素を削除
- stack.pop(0) # stack の先頭の要素を削除
- stack[-1]['opno'] = opno
解答選択欄
- c:
- d:
- e:
- f:
- g:
- h:
- i:
解答
- c=イ
- d=イ
- e=ウ
- f=エ
- g=オ
- h=ア
- i=ウ
解説
〔cについて〕
実行結果1で示されているように、関数 parse は引数として与えられた命令列を解釈し、タプルを要素とするリストに変換します。 parse ではPython独自の構文である"リスト内包表記"を用いています。これはリストを意味する[ ]の中にfor文を記述することで、リスト構造をコンパクトな記述で作成できる構文です。ここで登場する内包表記の意味は、
parse ではPython独自の構文である"リスト内包表記"を用いています。これはリストを意味する[ ]の中にfor文を記述することで、リスト構造をコンパクトな記述で作成できる構文です。ここで登場する内包表記の意味は、
「文字列 s を ; で分割してできたリストの要素数だけタプルを作る」
という意味になります。x には、命令列 s を ; で分割したときの各要素、すなわち個々の命令(F100やT90など)が入っています。
例えば文字列 s が命令列αの場合、s.split(';')の結果は、
['R3','R4','F100','T90','E0','F100','E0']
となります。そして上記の各々の文字列が、各々のタプルに変換されていきます。例えば、
'R3' → ('R',3)
'F100' → ('F',100)
という感じです。各命令は1文字目が命令コード、2文字目以降が数値パラメタですので、x[0] で命令の1文字目を取得し、数値パラメタはスライシングを用いて x[1:] と指定することで2文字目から文字列の最後までを取得できます。実行結果1を見るとタプルの2番目の要素は数値になっているので、 x[1:] を int() で型変換した「イ」が適切です。
∴c=イ:int(x[1:])
〔dについて〕
三角比に関する問題です。進行距離を斜辺n、マーカの進行方向 angle をθとすると、xとyの増減分(dx, dy)は以下のように表せます。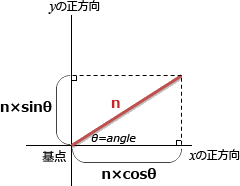 x軸方向の座標を決定するのはcos、y軸方向の座標を決定するのはsinです。sin(rad)とcos(rad)の正負はマーカの角度(angle)によって以下のように変化します。
x軸方向の座標を決定するのはcos、y軸方向の座標を決定するのはsinです。sin(rad)とcos(rad)の正負はマーカの角度(angle)によって以下のように変化します。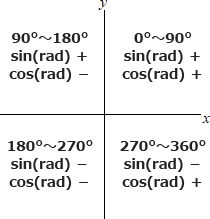 本問の座標系は右に進むとxが増加し、上にいくとyが増加するようになっているので、単純に math.cos(rad) と math.sin(rad) の組合せでxとyの増減分を計算できます。
本問の座標系は右に進むとxが増加し、上にいくとyが増加するようになっているので、単純に math.cos(rad) と math.sin(rad) の組合せでxとyの増減分を計算できます。
∴d=イ
〔eについて〕
以下の1文では4つの変数(x1, y1, x2, y2)にまとめて値を設定しています。
∴e=self.x, self.y
〔fについて〕
変数 insts には parse で作成した各命令をタプルとして保持するリストが格納されています。
forword()、turn() は、〔プログラムの説明〕(2)に記載されているように、引数として数値パラメタを受け取るので、fには val を指定することになります。
∴f=エ:val
〔g〕
関数 draw ではR命令による繰返し処理(以下、Rループとします)を、リスト(stack[])を用いたスタック構造で管理しています。
プログラムの流れを見ると、命令コード R を見つけると、スタックに {'opno':opno, 'rest':val} で表される辞書構造(連想配列)を積んでいます。opno は insts の先頭から数えた現在の命令番号、val はR命令の数値パラメタである繰返し回数です。
その後、命令コード E に到達するまで命令を順番に実行していきます。
命令コード E を見つけた場合、繰返し回数が残っていればRループの最初の命令に戻り、そうでなければRループから抜ける必要があります。hの次の行で、stack[] の末尾の要素(最後に積まれたデータ)の'rest'の値(繰返し回数)を1減じているので、こちらの分岐がRループを繰り返すときの処理とわかります。
分岐処理で'rest'の値を1減らしているのに、実行結果2で 'rest':0 が出力されていないことからも、「1より大きい」ことがRループの継続条件になっていることがわかります。
∴g=オ:>1
〔h〕
ここではRループの先頭に戻るための処理を行います。stack[-1]['opno'] には、Rループ開始場所の命令番号が格納されているため、現在の命令番号を示す opno を stack[-1]['opno'] で更新すれば、再度Rループの最初から命令から処理されます。
∴h=ア:opno = stack[-1]['opno']
〔i〕
ここではRループを終了するため処理を行います。実行結果2を見るとわかるように、'rest'の値が1になると stack[] の末尾の要素を削除しています。内側のループほど stack[] の後ろに格納されるためです。したがってiにはリストの末尾要素を削除する stack.pop() が入ります。
∴i=ウ:stack.pop()
実行結果1で示されているように、関数 parse は引数として与えられた命令列を解釈し、タプルを要素とするリストに変換します。

「文字列 s を ; で分割してできたリストの要素数だけタプルを作る」
という意味になります。x には、命令列 s を ; で分割したときの各要素、すなわち個々の命令(F100やT90など)が入っています。
例えば文字列 s が命令列αの場合、s.split(';')の結果は、
['R3','R4','F100','T90','E0','F100','E0']
となります。そして上記の各々の文字列が、各々のタプルに変換されていきます。例えば、
'R3' → ('R',3)
'F100' → ('F',100)
という感じです。各命令は1文字目が命令コード、2文字目以降が数値パラメタですので、x[0] で命令の1文字目を取得し、数値パラメタはスライシングを用いて x[1:] と指定することで2文字目から文字列の最後までを取得できます。実行結果1を見るとタプルの2番目の要素は数値になっているので、 x[1:] を int() で型変換した「イ」が適切です。
∴c=イ:int(x[1:])
〔dについて〕
三角比に関する問題です。進行距離を斜辺n、マーカの進行方向 angle をθとすると、xとyの増減分(dx, dy)は以下のように表せます。

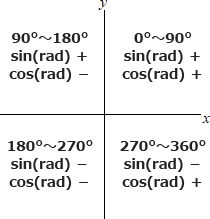
∴d=イ
〔eについて〕
以下の1文では4つの変数(x1, y1, x2, y2)にまとめて値を設定しています。
x1, y1, x2, y2 = e, self.x + dx, selfy + dy
続く olt.plot() で x1, y1, x2, y2 を使って線分を描画しており、その次の文ではマーカの位置を x2, y2 で更新しているので、x1, y1 には移動元の座標、x2, y2 には移動先の座標が入ることがわかります。eには x1, y1 に格納すべき値が入るので、マーカの現在位置を保持する2つのクラス属性 self.x, self.y が適切です。∴e=self.x, self.y
〔fについて〕
変数 insts には parse で作成した各命令をタプルとして保持するリストが格納されています。
code, val = insts[opno]
この処理では、タプルの値を先頭から順に code と val に格納しています。関数 parse のところで解説した通り、各タプルは(命令コード, 数値パラメタ)を保持しているので、code には命令コードが、val には数値パラメタが格納されます。forword()、turn() は、〔プログラムの説明〕(2)に記載されているように、引数として数値パラメタを受け取るので、fには val を指定することになります。
∴f=エ:val
〔g〕
関数 draw ではR命令による繰返し処理(以下、Rループとします)を、リスト(stack[])を用いたスタック構造で管理しています。
プログラムの流れを見ると、命令コード R を見つけると、スタックに {'opno':opno, 'rest':val} で表される辞書構造(連想配列)を積んでいます。opno は insts の先頭から数えた現在の命令番号、val はR命令の数値パラメタである繰返し回数です。
その後、命令コード E に到達するまで命令を順番に実行していきます。
命令コード E を見つけた場合、繰返し回数が残っていればRループの最初の命令に戻り、そうでなければRループから抜ける必要があります。hの次の行で、stack[] の末尾の要素(最後に積まれたデータ)の'rest'の値(繰返し回数)を1減じているので、こちらの分岐がRループを繰り返すときの処理とわかります。
if stack[-1]['rest'] g:
//Rループを繰り返すときの処理
h
stack[-1]['rest'] -= 1
else:
//Rループを抜けるときの処理
i
Rループを繰り返すのは周回数が残っているときです。実行結果2で'rest'の値の変化を見ると、'rest'が2以上のときは再度繰返し、1のときには stack[] の末尾の要素を取り除いていることがわかります。つまり、Rループの先頭に戻るのは'rest'の値が「1より大きい」場合となります。//Rループを繰り返すときの処理
h
stack[-1]['rest'] -= 1
else:
//Rループを抜けるときの処理
i
分岐処理で'rest'の値を1減らしているのに、実行結果2で 'rest':0 が出力されていないことからも、「1より大きい」ことがRループの継続条件になっていることがわかります。
∴g=オ:>1
〔h〕
ここではRループの先頭に戻るための処理を行います。stack[-1]['opno'] には、Rループ開始場所の命令番号が格納されているため、現在の命令番号を示す opno を stack[-1]['opno'] で更新すれば、再度Rループの最初から命令から処理されます。
∴h=ア:opno = stack[-1]['opno']
〔i〕
ここではRループを終了するため処理を行います。実行結果2を見るとわかるように、'rest'の値が1になると stack[] の末尾の要素を削除しています。内側のループほど stack[] の後ろに格納されるためです。したがってiにはリストの末尾要素を削除する stack.pop() が入ります。
∴i=ウ:stack.pop()
https://www.jitec.ipa.go.jp/1_00topic/topic_20191028.html
